introduction.

Ce travail fait suite à la thèse de William Beaudot : Le traitement neuronal de l’information dans la rétine des vertébrés. Jeanny Hérault et William Beaubot ont étudié des modèles de rétines qui se sont révélés particulièrement efficaces en vision artificielle. Notamment pour traiter la détection du mouvement. Ces modèles ont également donné lieu à des implantations sur circuits VLSI. Le projet de DEA s’appuie sur les modèles qui ont été construit précédemment et propose une modification de ceux-ci pour la vision de la couleur.

La particularité et l’originalité de l’équipe de recherche en neuromimétique est de fonder ses modèles par des constatations biologiques ou neurobiologiques. A partir d’une étude approfondie de la biologie de l’oeil, de la rétine et d’une partie du cerveau, nous construisons un modèle electrique simplifié. Les outils de traitement du signal nous permettent d’inférer sur le comportement du modèle et de confronter les résultats avec les études psychophysiologiques. Cette approche est à double avantage, elle permet d’engendrer des algorithmes simples pour la vision artificielle, et permet également de caractériser les éléments essentiels de la vision naturelle.

Le présent rapport s’articule en cinq chapitres. Le premier chapitre discute de la notion de couleur. Après un bref rappel de la physique de la lumière, nous décrivons les bases de la colorimétrie. La colorimétrie et la photométrie sont les théories fondamentales utilisées pour tous les travaux d’ingénierie qui concernent le traitement de la couleur. Ce chapitre est clos par différents aspects psychophysiologiques de la vision des couleurs.

Le chapitre suivant traite de la biologie du système visuel. Nous rappelons l’anatomie de l’oeil et celle de la rétine en insistant sur le rôle des récepteurs. Nous décrivons brievement les mesures qui ont été faites pour les réponses des différentes cellules à la couleur.

Dans le chapitre 3, nous présentons les modèles de rétine. La première partie de ce chapitre présente la différence d’approche entre les modèles classiques en traitement d’images et les modèles neuromimétiques. Ensuite nous présentons les différents modèles de rétine construit par Jeanny Hérault et William Beaudot. Nous étudions en détail leur construction à partir des modèles du neurone et des connexions synaptiques. Ensuite nous détaillons les comportements fréquentiels des différentes variantes du modèle de base. Finalement nous présentons un nouveau modèle qui semble biologiquement plus réaliste.

Le quatrième chapitre est entièrement consacré aux modèles de rétine en couleur. Les modèles de rétine en couleur que nous avons développé sont sur maillage hexagonal. Nous commençons par l’étude de l’espace dual du maillage hexagonal en fréquence. Cette étude est indispensable pour comprendre le sous-échantillonnage chromatique de la couche des cônes. Ensuite nous détaillons les différentes propriétés psychophysiologiques principales de ces modèles.

Finalement le cinquième chapitre explique l’implantation des modèles de rétines sur maillage hexagonal dans le simulateur de rétine que nous avons conçu durant ce stage.

CHAPITRE 1 :

NOTION DE COULEUR.

« Plus on rêve à ce monde, plus on pense que les couleurs ont été faites pour qu’il soit beau. Et la beauté n’est pas une ruse, c’est un besoin pour l’homme. »

Yves Le Grand 1956.

La couleur est une qualité du système visuel humain que partage également certaines espèces animales comme les écureuils, les primates ou les oiseaux, contrairement à d’autre espèce comme les chiens, les lapins, les souris et en général les espèces diurnes, qui en sont privées.

L’étude de la couleur a été entreprise depuis de nombreuses années, elle reflète très certainement des besoins naturels liés à la survie de l’espèce [1], comme la recherche de nourriture. La reproduction de la sensation de couleur est un domaine qui a connu un fort développement (photométrie, colorimétrie), et qui est en mesure de fournir des procédés industriels très performants. Dans ce chapitre nous allons tout d’abord effectuer un rappel des notions de base, puis nous aborderons la description de certains effets du système visuel humain, relatif à la couleur.

1.1. eMISSION-ABSORPTION-reflexion-transmission.

La couleur est subjective, elle n’a pas de réalité physique proprement dite. Elle résulte d’une interprétation par le système visuel du spectre de longueurs d’onde composant la lumière se projetant sur l’oeil. De fait, l’étude du comportement des lumières colorées se résume à l’étude des modifications du spectre de la lumière, le long du parcours de sa source d’émission, à sa réception dans l’oeil.

La nature physique de la lumière est issue de la matière. Les électrons gravitent autour du noyau, la configuration des électrons autour du noyau représente un état. L’absorption par un atome de l’énergie apportée par une radiation ou un champ électrique, donne lieu au saut d’un électron de son orbite à une orbite supérieure. L’atome se trouve alors dans un état excité. De la même manière, le passage d’un atome d’un état excité à un état stable est caractérisé par une émission d’un rayonnement électromagnétique de fréquence , faisant apparaître dans le spectre une raie d’émission. Cette raie peut-être dans le domaine visible ou non.

Figure 1. 1 : Représentation de la sensation de couleur en fonction de la longueur d’onde .

Le passage entre deux niveaux d’énergie, et , a comme résultat l’émission d’une quantité d’énergie appelée photon suivant la relation :

(1.2.1)

Cette dernière relation fait apparaître la nature duale de la lumière, qui peut être considérée suivant les cas, comme une émission de particules d’une certaine énergie, et dans d’autres comme un rayonnement électromagnétique de fréquence donnée. L’approche corpusculaire permet d’expliquer des phénomènes tel que l’effet photoélectrique tandis que l’approche ondulatoire permet d’expliquer les phénomènes d’interférence, de diffraction de la lumière. Le lien entre ces deux théories peut-être fait en considérant que la probabilité de la présence d’un photon en un point donné est proportionnelle au carré de l’amplitude à cet endroit de l’onde correspondante. Dans ce travail l’aspect qui nous intéresse correspond à l’étude de l’évolution du spectre, donc à la nature ondulatoire de la lumière.

L’émission de rayonnement électromagnétique est en général continue, résultant de rayonnements thermiques. En effet, suivant leur température, tous les corps émettent des radiations, de composition spectrale différente, d'où le terme de température de couleur. L’énergie résultante de l’émission dépend de la fréquence de la raie émise et de la température du corps. Le bilan énergétique entre l’énergie émise et l’énergie absorbée est constant pour tous les corps, la première dépend de la température et la deuxième de la longueur d’onde. Une autre forme d’émission appelée fluorescence et phosphorescence se caractérise par des sauts orbitaux des électrons non émissifs qui conduisent à une émission ‘retardée’ lors du retour de l’électron à son état de base. Cette émission est alors à spectre de raie.

La transformation du spectre lumineux est également caractérisée par deux phénomènes : la réflexion et la transmission. La réflexion représente la distribution du spectre incident qui est renvoyé par le corps. On distingue alors la réflexion spéculaire (effet miroir) de la réflexion lambertienne (effet diffusant). La transmission caractérise les corps transparents ou translucides qui agissent par filtrage du spectre incident.

1.2. vision trichromatique.

De nombreuses études ont montré que la transcription d’une image projetée sur l’oeil en sensation de couleur, se faisait par l’intermédiaire de trois types de récepteurs. Chacun de ces types de récepteurs est doté d’une sensibilité spectrale différente. Nous verrons dans le chapitre suivant que ce n’est pas le cas pour certains individus qui seraient dotés d’une vision en tetrachromie ou en pentachromie. Il est fort probable également que, parmi les individus qui sont dotés de trois type de récepteurs, ceux-ci n’aient pas des réponses identiques à la longueur d’onde[1].

1.2.1 Expérience d’égalisation.

La nature trivalente de la vision est également observée dans les expériences d’égalisation de la couleur qui sont à la base de la colorimétrie [2].

(a) (b) (c) (d)

Figure 1. 2 : Les quatre expériences d’égalisations (a)(b)(c)(d) mettent en évidence la nature trivalente de la vision

Pour la première expérience d’égalisation (Figure 1. 2-a), on présente au sujet une lumière colorée [W] non monochromatique projetée sur un écran. Celui-ci essaye de reproduire la couleur sur un autre écran juxtaposé à l’aide de trois boutons de réglage d’intensité des couleurs de [A], [B] et [C]. Si les couleurs réglables [A], [B] et [C] sont suffisement différentes[2], on vérifie que le sujet réussit à reproduire la luminance et la chromaticité de la couleur de base. L’expérience est également possible pour des couleurs de base à spectre de raie.

La deuxième expérience d’égalisation montre que si la couleur de référence est à spectre très étroit, l’égalisation est possible si l’on déplace une des couleur réglable [A], [B] ou [C] du coté de la couleur de référence [W]. Plus précisement le sujet manipule l’intensité de [A], [B] et [C] pour obtenir l’égalisation de [W]+[C] par exemple (Figure 2-b). L’apparence de la plage de droite dans ce cas est également modifiée. Cette expérience revient à considérer que les réglages de couleur peuvent être négatifs.

La troisième montre que si l’on possède plus de trois sources réglables, il y a redondance et plusieurs combinaisons mènent au même résultat. La quatrième expérience montre qu’il est en général impossible, à partir de deux couleurs réglables, d’obtenir la couleur de référence. L’égalisation n’est possible que si la couleur de référence est un combinaison des deux couleurs réglables.

A partir de ces résultats, il est possible d’établir une algèbre de la couleur. Désignons par [X] le spectre en valeur relative de la couleur X, et x[X] la couleur X à luminance x. Les expériences d’égalisation nous permettent d’écrire pour toute couleur W :

W = a[A]+b[B]+c[C] (1.2.1)

Avec [A], [B], [C] couleurs primaires et a, b, c quantités de ces couleurs primaires, qui peuvent être négatives.

A cette loi d’équivalence, nous pouvons ajouter les lois de composition suivantes :

· Aditivité : L’ajout de la même quantité x de couleur X ne modifie pas l’équivalence.

si a[A]=b[B] alors a[A]+x[X]=b[B]+x[X] (1.2.2)

· Proportionnalité : En multipliant la luminance de chaque couleur à l’équivalence on ne modifie pas celle-ci.

si a[A]=b[B] alors ka[A]=kb[B] (1.2.3)

1.2.2 Systèmes de représentation de la couleur.

Les lois énoncées dans le paragraphe précédent nous permettent d’établir une méthode de représentation des couleurs basées sur un espace à trois dimensions dont les vecteurs de base sont les trois couleurs de base, et les coordonnées d’une couleur quelconque sont données par la valeur des intensités de chaque couleur de base à l’équivalence.

Il est habituel de considérer les trois couleurs primaires comme étant le rouge pour celle qui se trouve la plus à droite du spectre des couleurs, le vert pour la couleur centrale et le bleu pour la couleur la plus à gauche. Cependant la sensation colorée pour ces primaires peut être différente de la dénomination.

(a) (b)

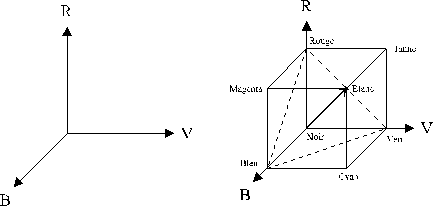
Figure 1. 3 : (a) Espace RVB (b) Position des couleurs dans l’espace RVB. L’axe en gras est achromatique, il correspond à la même quantité de R,V et B. Le triangle en pointillé est appelé triangle de Maxwell et contient l’ensemble des couleurs à luminance constante.

Nous voyons que le choix des axes RVB conditionne l’apparence des couleurs, par exemple la valeur de la lumière blanche. Nous pouvons représenter n’importe quelle couleur dans ce système RVB, ceci par le principe d’égalisation. Nous pouvons également représenter l’addition de couleur.

(a) (b)

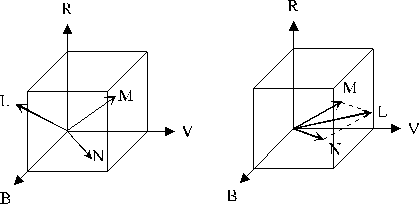
Figure 1. 4 : (a) Représentation des différentes couleurs dans l’espace RVB. La couleur L a des composantes négatives, cela signifie quelle ne peut pas être obtenue par simple addition des couleurs de base. (b) Représentation de l’addition des couleurs (L=M+N).

Il existe une infinité d’espaces RVB, différentiés par le choix des trois couleurs primaires. La Commission Internationale de l’Eclairage C.E.I. a normalisé les trois couleurs de base de l’espace RVB permettant de réduire l’artifice de l’utilisation des couleurs négatives pour permettre l’égalisation avec n’importe quelle couleur de référence. Le système de représentation est appelé XYZ. Le spectre de luminance des couleurs de base X, Y et Z est donné sur la figure suivante. On remarque pour la couleur x que la luminance est négative, cette couleur n’a donc pas de réalité physique. Il s’agit de primaires virtuelles.

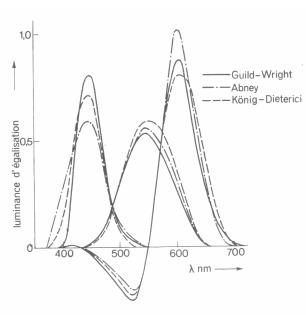
Figure 1. 5 : Trois mesures différentes des luminances d’égalisation. Celle de Guild et Wright sert de référence pour la Commission Internationale de l’Eclairage [3].

Un autre système de représentation de la couleur a également été développé pour faciliter la composition des couleurs. Il s’agit de la représentation TLS (Teinte Luminance et Saturation).

Figure 1. 6 : Système de représentation TLS. Teinte, Luminance, Saturation.

Il existe deux méthodes pour la synthèse des couleurs. La synthèse additive, comme pour les expériences d’égalisation, consiste à superposer des sources colorées de manière à engendrer une nouvelle couleur. La synthèse soustractive est obtenue par soustraction de bandes de couleurs à la lumière blanche, à l’aide de filtre. Par exemple la télévision couleur fonctionne en synthèse additive, alors que la projection de diapositive est une synthèse soustractive. Les primaires en synthèse additive sont le rouge, le vert et le bleu. Alors qu’en synthèse soustractive ce sont le cyan, le magenta[3] et le jaune.

1.3. Apparence des couleurs.

Nous avons déjà parlé dans le paragraphe précédent de l’apparence des couleurs, il reste à préciser que celle ci dépend également de la réponse spectrale des récepteurs de la rétine. Cependant cet aspect sera développé dans le chapitre suivant. Nous voudrions exposer dans ce paragraphe la variabilité de l’apparence des couleurs suivant les conditions d’observation et l’adaptation chromatique de la rétine.

1.3.1 Conditions d’observations.

L’effet des conditions d’observation est très important : d’une part la sensation colorée peut sembler différente pour une même stimulation physique, d’autre part une même sensation colorée peut faire intervenir des stimulations différentes (couleurs métamères).

1.3.1.1 Effet coloré dû à la luminance.

La chromaticité dépend tout d’abord de l’intensité d’éclairement. On distingue trois types de vision pour l’homme : scotopique pour la vision de nuit, mésotopique pour de faibles éclairements journaliers, et la vision photopique pour une journée ensoleillée [4]. La courbe de sensibilité des cônes et des bâtonnets permet d’expliquer la modification des couleurs, pour ces différents cas de figure. Bien que la mesure des seuils de vision soit rendue difficile par les phénomènes d’adaptation à la luminance, on remarque que les bâtonnets sont extrêmement sensibles et saturent lors d’un fort éclairement, tandis que les cônes n’ont pas de sensibilité suffisante en vision scotopique. Les cônes et les bâtonnets interviennent donc différement suivant la quantité d’éclairement.

La différence des visions photopique et scotopique donne lieu au phénomène de l’effet Purkinje, découvert en 1825. Des plages de couleur rouge, verte et bleu qui paraissent à luminance semblable en vision photopique, vont se distinguer par leur luminance en vision scotopique. La plage rouge parait complètement noire, alors que les plages vertes et bleues paraissent grises.

Un autre effet se fait sentir à forte luminance, juste au-dessous du seuil d’éblouissement. On observe un changement de l’apparence des couleurs par forte augmentation des luminances, les rouges ont tendance à se changer en jaune, alors que les violets et bleus-verts se changent en bleu. C’est l’effet Bezold-Brucke.

Le dernier effet coloré dû à la luminance apparaît lorsqu’on ajoute une lumière blanche, uniforme, à une couleur donnée. Il s’associe à la désaturation de la couleur une légère variation de teinte. C’est l’effet d’Abney [5]. Pour tenir compte de cet effet en représentation TLS par exemple, il faut courber l’axe des luminances, lorsque celles-ci deviennent grande.

1.3.1.2 Effet coloré dû au champ environnant.

La perception de la couleur en un point visé dépend fortement du champ environnant. Si l’on présente par exemple deux zones de même couleur, bordées de deux zones de couleur différentes (en intensité ou en chromaticité), les zones semblables paraissent différentes.

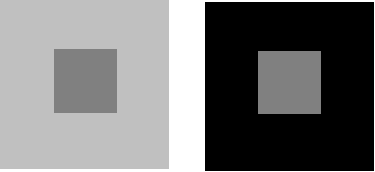
Figure 1. 7 : Effet dû au champ environnant. Influence de la luminance des grands carrés, sur la perception de couleur du petit. Cette expérience est transposable pour des zones colorées.

Cette influence des luminances de la plage du centre par rapport au fond à été étudiée par Hunt [6]. Les mesures effectuées par Helson et Michels [7] montrent que la teinte du champ environnant, surtout s’il est plus lumineux que la plage visée, induit dans cette dernière une réponse antagoniste qui déplace sa teinte vers son complémentaire.

Brown [8] a montré également qu’un fond dont la teinte est complémentaire à la teinte observée, réduit la capacité de l’oeil à détecter des variations de teinte et de saturation. Au contraire avec un fond de teinte voisine la capacité de discrimination des teintes et saturation de la plage observée s’en trouve fortement grandie.

1.3.1.3 Effet McCollough.

Un autre effet mis en évidence par McCollough , fait un lien entre couleur et orientation. Ce lien serait fait au niveau de l’aire V1, et nous proposerons un modèle dans le chapitre 4. Nous allons dans ce paragraphe expliquer en détail l’expérience réalisée pour mettre en exergue cet effet.

L’expérience se déroule en deux étapes. Au cours de la première on présente au sujet une grille composée de traits verticaux colorés en rouge, alternativement à une grille de traits horizontaux colorés en vert. Pendant un temps donné le sujet va observer successivement l’une et l’autre grille. Après cette phase d ’habituation, on présente au sujet deux grilles de couleurs blanches, orientées verticalement et horizontalement, celui-ci va avoir l’impression que la grille verticale sera colorée en cyan et la grille horizontale en majenta.

Cet effet met en évidence un système d’inhibition latérale entre orientation et couleur. Des études ont été poursuivies au laboratoire : Boubakar compare les temps de recherche d’une cible colorée et orientée dans une texture également colorée et orientée avant et après l’induction par l’effet McCollough. La faculté de reconnaissance des cibles est améliorée si l’induction à eu lieu pour l’orientation et la couleur complémentaire à la cible cherchée.

1.3.1.4 Constance de l’apparence des couleurs.

La constance des couleurs nomme la relative constance de la discrimination des teintes, pour des sources de lumières à couleurs différentes. Helmholtz montre qu’on observe une constance des apparences des couleurs, indépendemment de l’éclairage donné. En s’habituant très rapidement à la couleur d’un éclairage différent, l’observateur fait entièrement abstraction du changement de teinte général de son champ visuel et considère l’éclairement comme étant blanc.

Les travaux de Wright montre que la constance de l’apparence des luminosités est liée aux phénomènes d’adaptation, il en va de même pour la constance des couleurs. Ce dernier a mesuré le rapport entre un éclairement rétinien utilisé à l’adaptation et l’éclairement rétinien donnant une même sensation de luminance après adaptation. Ce rapport est constant sur presque toute la gamme d’éclairement.

1.3.2 Adaptation chromatique

L’adaptation en général est un fait important de la vision naturelle. L’adaptation peut se faire par rapport aux fréquences spatiales (Aude Olivia [15]), aux orientations, à la luminance ( W.Beaudot [11]) et à la chrominance. Nous pensons que ces phénomènes d’adaptation ont pour objet d’augmenter la sensibilité aux événements visuels pertinents dans une scène. En effet les phénomènes d’adaptation ont pour effet de diminuer la réponse aux stimulis constants en s’opposant à ceux-ci, il s'ensuivra une réponse forte pour des stimulis nouveaux à la scène d’adaptation.

L’adaptation chromatique déplace les teintes observées vers leurs teintes complémentaires. Ceci peut être observé par le phénomène de désaturation d’une teinte. Si l’on présente une teinte pendant un certain temps, lors de l’extinction de cette teinte le sujet verra apparaître la teinte complémentaire en décroissance de luminosité.

G.Buchsbaum et A.Gottschalk de l’université de Pennssylvania aux Etats-Unis présentent un modèle de l’adaptation visuelle comme réducteur de la quantité d’information visuelle à transmettre à travers le nerf optique. Leur modèle est fondé sur le diagramme suivant et garanti la minimisation par un calcul approprié des coefficients W.

Figure 1. 8 : Représentation du modèle de l’adaptation chromatique de Buchsbaun et Gottschalk. S() représente le signal projeté sur la rétine. B(),V(), R() les courbes de sensibilité des trois récepteurs et A, P, Q les signaux d’opposition de couleur. L’adaptation se fait à travers les poids W.

Une méthode pour rendre les trois signaux d’opposition de couleur A, P et Q décorrélés consiste à utiliser la transformation en vecteur propre. Cette transformation réalise une diagonalisation de la matrice des covariances entre les signaux de couleur à la sortie de B, V, R. Cette diagonalisation rend alors nulle les intercorrélations entre les signaux A, P, Q. Cette pratique ressemble beaucoup au modèle de la séparation de sources que nous présenterons au chapitre 4, bien qu’ici la modification des coefficients W ne soit pas explicitée.

Nous reprochons également à ce modèle le manque de validité biologique par rapport au traitement rétinien et nous proposerons au chapitre 4, une variante du modèle de rétine qui peut tenir compte de l’adaptation chromatique.

Chapitre 2 :

biologie du systeme visuel.

Nous allons décrire brièvement, dans ce chapitre, la biologie du système visuel. Celui-ci est particulièrement complexe et de nombreux articles issus de la biologie en font une description. Ce chapitre a pour objet de réunir les fondements pour les modèles de rétine que nous allons faire par la suite.

1.4. L’oeil.

Plus qu’un simple récepteur, l’oeil contribue de manière active à la vision. Nous considérons que le travail de l’oeil s’apparente au traitement de bas niveau d’une image, et conditionne la suite du traitement par le cerveau.

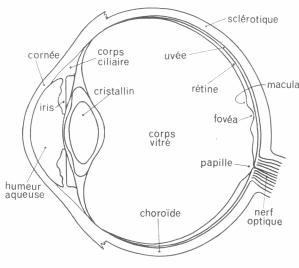
Figure 2. 9 : Coupe horizontale de l’oeil humain[3].

De forme approximativement sphérique, l’oeil comporte des éléments destinés à recevoir le rayonnement incident. Elément optique pour former une image, éléments neuraux pour traiter l’information recueillie. L’optique est réalisé par la cornée, la pupille et le cristallin.

La cornée contribue par sa forme bombée à la puissance optique de l’oeil, la partie frontale de la cornée est appelée sclérotique. La pupille est le trou dont est percé l’iris. Le diamètre de la pupille est variable pour permettre une accommodation. Le cristallin s’apparente à une lentille, il est permet la projection de l’image sur la rétine. Ce dernier, plaqué contre l’iris, est suspendu par des fibres musculaires qui le déforme pour envoyer une image nette à la surface de la rétine quelque soit la distance de l’objet.

Le volume intérieur de l’oeil contient la gelée transparente du corps vitré. Celui-ci est entouré de l’uvée qui absorbe les rayons lumineux ayant traversé la rétine. Tapissée sur l’uvée se tient la rétine, chargée tout d’abord de transformer les signaux lumineux en signaux électriques, puis de les traiter et ensuite de les transmettre aux zones visuelles supérieures à travers le nerf optique. La structure de la rétine est très changeante avec l’éloignement de l’axe optique. On retrouve trois zones essentielles. La macula, tache jaune située proche de l’axe optique, contient en son centre la fovéa, partie la plus sensible de la rétine. La papille est le départ du nerf optique, cette partie est dépourvue de récepteurs et constitue la tache aveugle.

Le système optique n’est pas parfait et produit des aberrations. Celles-ci sont de deux types, aberrations chromatiques et aberrations géométriques. Les aberrations chromatiques sont dues à la différence de l’indice de réfraction de l’onde lumineuse avec sa fréquence. Alors que les aberrations géométriques viennent de l’imperfection du cristallin lorsque le rayon incident arrive loin de l’axe. Les aberrations géométriques seraient essentiellement corrigées par la forme circulaire de l’oeil.

L’oeil n’est pas fixe, au contraire il est sans arrêt en mouvement. Les saccades sont des mouvements brusques des 2 yeux, d’un angle de 2 à 25 minutes d’angle et de durée de 100 à 200 ms. Les micro-saccades sont des mouvements d’amplitude beaucoup plus petit ( <1 minute) qui correspondent à des tremblement et de fréquences voisines de 150Hz. Ces mouvements impliquent que l’image n’est jamais fixe dans la rétine. Il semble que l’amplitude des saccades soit controlée, alors que les micro-saccades seraient autonomes.

1.5. La retine.

La rétine est un système neuronal de traitement. Elle est composée de plusieurs couches, chacune possédant une grande population de neurones. La première fonction de la rétine est de transformer les signaux lumineux en signaux électriques, c’est le travail des photorécepteurs. Ensuite le traitement neuronal des autres couches a des fonctions différentes et encore partiellement connues. Nous distinguons l’étude de la PLE (couche plexiforme externe) composée des cellules horizontales et bipolaires, de la PLI ( couche plexiforme interne) composée de cellules amacrines et ganglionnaires.

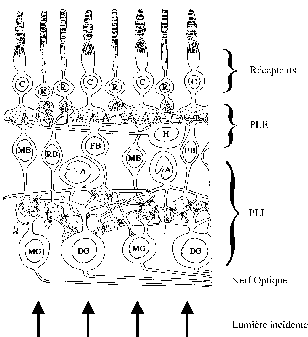
Figure 2. 10 : Structure de la rétine humaine. B bâtonnets, C cônes, H cellules horizontales, XB Différents types de cellules bipolaires, A cellules amacrines, XG Différents type de cellules ganglionnaires.

1.5.1 Les récepteurs.

Les récepteurs sont deux types, bâtonnets et cônes. Les bâtonnets ont une très grande sensibilité qui les rend fonctionnels en vision scotopique et saturent en vision photopique, contrairement aux cônes. Les bâtonnets ne possèdent qu’un seul type de réponse spectrale alors que les cônes en ont trois.

(a) (b)

Figure 2. 11 : (a) Coupe schématique d’un bâtonnet de mammifère obtenue à partir de l’observation au microscope électronique. (b) Absorption moyenne des trois pigments de cônes humains [3].

Les extrémités des cônes et bâtonnets des mammifères ont une structure très spécifique. Elles contiennent de nombreux disques minces à bords dentelés empilés perpendiculairement à leur longueur. Ces piles de lamelles sont ensuite reliées aux segments internes par des cils de connexions contenant des granulations de formes cylindriques entourées de minuscules tubes. La structure interne des cônes est différente de celle des bâtonnets.

Le fond de l’oeil contient des pigments qui se décolorent rapidement par exposition à la lumière. Ces pigments ont été identifiés comme la rhodopsine pour les bâtonnets, la cyanoblade pour le récepteur bleu, la chloroblade pour le vert et l’erythroblade pour le rouge. Plusieurs techniques récentes ont permis d’étudier ces pigments : étude chimique et spectrophotométrie des pigments extraits [17], spectrophotométrie de la lumière réfléchie par le fond de l’oeil vivant [18] et mesure des absorptions des pigments contenus dans les cônes et bâtonnets de rétine fraîchement extraite [19]. Ces différentes méthodes donnent des résultats semblables et confirment l’hypothèse d’une seule caractéristique de pigments pour les bâtonnets. Celui-ci a un spectre d’absorption maximal pour la couleur pourpre rétinien de longueur d’onde 502 nm. Elles confirment également l’existence de trois pigments différents pour les cônes, d’absorption maximale bleue à 445 nm, verte à 535 nm et rouge à 570 nm (figure 3).

La décoloration des pigments à la lumière est très rapide, de sorte que les saccades et micro-saccades semblent indispensables pour changer sans arrêt le champ visuel des récepteurs. Une expérience à d’ailleurs montré que si l’on maintient fixe l’image rétinienne, le sujet la voit disparaître en quelque seconde pour laisser place à une image grise puis complètement noire. La même expérience à été appliqué à deux plages de couleur. Elle montre que la couleur des deux plages tend à s’uniformiser vers la couleur moyenne avant de disparaître.

J.Tovée [1] explique que certains gènes sont responsables du codage des pigments visuels. La génétique permet alors de conprendre certaines défaillances visuelles comme le daltonisme. Mais le fait le plus remarquable est que par les même procédés on montre que la vision de certains individus serait basée sur plus de trois récepteurs. En particulier les femmes qui posèdent des chromozomes X pourraient possèder une vision tétrachromique ou pentachromique. J.Tovée remarque cependant que la vision en tétrachromie ou pentachromie ne dépend pas seulement des récepteurs, mais également de la prise en compte de ces récepteurs pour le traitement dans son essemble. Et ceci est fort peu probable si les récepteurs suplémentaires sont en infériorité numérique.

La rétine contient entre 110 à 125 millions de bâtonnets et de 4 à 7 millions de cônes. Les cônes sont essentiellement présents en fovéa centrale. Ils atteignent une proportion de 147000 par millimètre carré pour un angle visuel d’un demi-degré. pour diminuer rapidement à une proportion 5000 par millimètre carré vers 10 degrés. Les bâtonnets sont complètement absents au centre de la fovéa (1/2 degré), mais atteignent une proportion de 160000 par millimètre carré vers 20 degrés qui diminue ensuite. Les cônes sensibles au bleu sont beaucoup moins nombreux (1/3) que ceux sensibles au vert et au rouge.

Les cellules réceptrices sont essentiellement connectées avec les cellules horizontales et bipolaires. Ces connexions sont réalisées par des liaisons synaptiques chimiques et réciproques. Des couplages de type synapse gap-junction entre récepteurs sont également présents. Les bâtonnets sont reliés entre eux. Les cônes sont également connectés entre eux avec la particularité de connexions uniquement entre cônes de même type. Cette dernière caractéristique est un point essentiel du modèle de rétine en couleur étudié au chapitre 4. Les cônes de la zone fovéale centrale sont directement connectés aux cellules ganglionnaires dont les axones forment le nerf optique. Cette caractéristique est sans doute importante pour la vision des couleurs.

1.5.2 La PLE.

La couche plexiforme externe est composée de deux types de cellules : les cellules appelées horizontales car elles ont des connexions horizontales avec les autres cellules le long de la rétine, les cellules bipolaires qui sont hyperpolarisantes ou dépolarisantes.

A l’intérieur des cellules horizontales, on distingue deux catégories. Les cellules horizontales sans axone qui ont d’épaisses dendrites qui entrent en contact avec les cônes le long de la rétine et opèrent une action sur les bipolaires de cônes. Les cellules horizontales avec axones qui assurent une connexion cônes-bâtonnets (figure 2.2).

Le champ récepteur des cellules horizontales est large à cause de la longueur des connexions de ces cellules avec les récepteurs. Des expériences faisant varier la longueur d’onde de la stimulation ont réussi à montrer une spécialisation des cellules horizontales pour la couleur. Un premier groupe répond de manière semblable à la courbe de réponse des récepteurs et sont appelées cellules horizontales de luminance. Un autre groupe a des profils de réponse du type biphasique, hyperpolarisé au rouge (R+) et dépolarisé au vert (G-) ou l’opposé (R-) et (G+), ou (R+)/(B-) ou (R-)/(B+). Le dernier groupe a un profil triphasique de type (R+)/(Y-)/(B+) [20].

Les cellules bipolaires sont différentiées par la taille de leur champ dendritique, le récepteur contacté et la nature du contact synaptique. On distingue :

· Les bipolaires des bâtonnets, qui ont un champ dendritique large, et qui contactent un grand nombre de bâtonnets par un contact invaginant.

· Les bipolaires naines qui ont un champ dendritique étroit, et ne contactent qu’un seul cône, par une synapse invaginante ou superficielle.

· Les bipolaires plates qui ont un champ dendritique moyen, et contactent plusieurs cônes par synapses plates.

La polarité de la réponse produite par les bipolaires sont de deux types hyperpolarisantes ou dépolarisante. Les bipolaires hyperpolarisantes ont une réponse à champ central OFF et périphérique ON, alors que les dépolarisantes ont une réponse à champ centrale ON et périphérique OFF. Pour la vision des couleurs les champs récepteurs des cellules bipolaires sont à antagonisme chromatique simple ou chromatique double.

La structure des liaisons entre cellules réceptrices, horizontales et bipolaire est appelée triade synaptique. Dans cette structure les cellules horizontales ont une action inverse des cellules réceptrices sur les cellules bipolaires. Ce mécanisme engendre une inhibition latérale responsable de l’antagonisme centre-périphérie au sein des bipolaires (figure 3.6).

1.5.3 La PLI.

La couche plexiforme interne est essentiellement composée de cellules amacrines jouant le même rôle que les cellules horizontales pour la PLE et de cellules ganglionnaires dont les axones forment le nerf optique. Les fibres du nerf optique sont au nombre de 1 million ce qui est 5 fois inférieure au nombre de cônes et 100 fois inférieure à celui des bâtonnets. Le traitement de la rétine doit permettre cette réduction d’information.

Les cellules amacrines sont dépourvues d’axones, mais leurs dendrites s’étendent au niveau de l’articulation entre les bipolaires et les ganglionnaires. On ne distingue pas différentes réponses des cellules amacrines en fonction de la longueur d’onde. Par contre on distingue la réponse constante des amacrines toniques de la réponse transitoire des amacrines phasique pour une stimulation constante.

Dans la même couche que les amacrines on repère une autre variété de cellules appelées cellules interplexiformes dont les prolongations se projettent dans la PLE et dans la PLI. Ces cellules entrent en contact avec les bipolaires et les cellules horizontales, réalisant ainsi une rétroaction de la PLI sur la PLE. Ces cellules libèrent de la dopamine au niveau des horizontales. La dopamine à pour effet de diminuer la capacité des cellules horizontales à entretenir l’antagonisme centre-périphérie sur les cellules bipolaires. Ces cellules sont reliées aux cellules ganglionnaires et pourraient réintroduire dans la PLE des informations transitant sur le nerf optique. Ce phénomène est responsable d’une partie de l’adaptation de la rétine.

Les cellules ganglionnaires se divisent en trois types suivant la taille de leur soma. Les cellules Ga qui ont un soma de grande taille, une arborisation dendritique étendue et riche, un axone de gros diamètre à conduction électrique rapide. Les cellules Gb avec un soma plus petit, un axone fin à conduction lente et un champ dendritique restreint. Les Gg ont un champ dendritique étendu mais clairsemé. L’évolution de la taille du champ dendritique des cellules ganglionnaires est une fonction quasiment linéaire de l’exentricité. Par conséquent, les cônes sont préférentiellement liés aux cellules ganglionnaires de petite taille, contrairement au bâtonnets. La réponse des cellules ganglionnaire à un stimulus se distingue selon trois cas : Les ganglionnaires ON qui répondent à l’établissement du stimulus, les ganglionnaires OFF qui répondent à son extinction et enfin les ganglionnaires ON-OFF qui répondent à la fois à l’apparition et à l’extinction du stimuli.

La réponse à un stimulus de couleur des cellules ganglionnaires a également été étudiée. On trouve des cellules à antagonisme centre périphérie R/G qui se décompose en quatre catégories (R+/G-) 21%, (G+)/(R-) 11%, (R-)/(G+) 5%, (G-)/(R+) 9%. On trouve également des antagonismes de type B/L dans les proportions suivantes (B+)/(L-) 5.7% et (B-)/(L+) 0.3%, où L représente la luminance.

Les connexions entre les deux types de cellules bipolaires, dépolarisante et hyperpolarisante, et les cellules ganglionnaires de type, ON et OFF, respectent une symétrie. Les bipolaires dépolarisantes sont connectées au ganglionnaires ON, alors que les bipolaires hyperpolarisante sont connectées au ganglionnaires OFF. On trouve alors deux circuits de connexions indépendants, suivant lesquels transitent des signaux opposés ON et OFF. Dans le modèle de rétine étudié par la suite nous n’avons pas tenu compte du circuit OFF, mais seulement du ON.

1.6. Le cgl et les aires corticales.

Après avoir été traités par la rétine, les signaux sont envoyés vers les aires corticales. Mais avant cela la majorité des axones des cellules ganglionnaires aboutissent dans le corps genouillé latéral (CGL). Ce dernier a une structure qui respecte la topologie de la rétine, des fibres voisines dans la rétine aboutissent sur des cellules voisines dans le CGL. Au niveau du CGL et du cortex les canaux de l’oeil gauche et de l’oeil droit sont réunis.

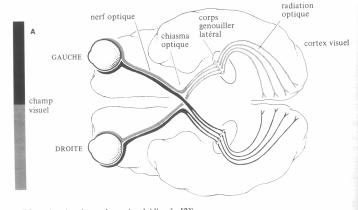
Figure 2. 12 : Description générale du système visuel.[9]

Le corps genouillé latéral est composé de 4 couches de petites cellules appelées parvocellulaires et 2 couches de grosses cellules appelées magnocellulaires. En injectant un traceur radioactif on montre que les fibres issues de l’oeil droit et celles issues de l’oeil gauche ne sont pas mélangées et activent des couches alternées de neurones. L’antagonisme chromatique est encore augmenté. On trouve des cellules à antagonisme rouge/vert et bleu/jaune.

Après avoir été acheminés par le corps genouillé latéral, les signaux sont envoyés dans le cortex visuel. A l’intérieur de celui-ci nous pouvons distinguer le cortex strié, encore appelé aire 17 ou aire V1. Lui-même est divisé en 6 couches numérotées I à VI. Les fibres issues du corps genouillé latéral se projettent sur la couche IV, elle même stratifiée suivant que les axones proviennent des cellules magnocellulaires ou parvocellulaires, ou appartiennent au système ON ou OFF. Le marquage de l'aire IV laisse apparaître des groupes de cellules à champ récepteur à antagonisme spatial L+/L-, à double antagonisme rouge/vert et à double antagonisme jaune/bleu [21].

Figure 2. 13 : Structure du cortex strié du chat [10].

Schématiquement le cortex apparaît structuré en petites colonnes. Chacune de ces colonnes étant sensible a des orientations et des fréquences spatiales particulières ou à des orientations et opposition de couleurs particulières. Dans le chapitre 4 nous proposons un modèle de séparation de sources des informations d’orientation et de couleur, qui permet d’expliquer le fonctionnement de l’effet McCollough.

A l’avant du cortex strié se trouve les aires 18 et 19. L’aire 19 est particulièrement sensible à la couleur. Certaines des cellules de l’aire 19 répondent sélectivement à la longueur d’onde, alors que d’autres perçoivent des plages de couleurs d’une surface.

Chapitre 3 :

Modèles de rétine.

Il existe un grand nombre d’algorithmes en traitement d’image pour la détection des contours, la squelettisation des formes, la détection du mouvement, le traitement bas niveau d’image en général. La plupart de ces méthodes se construisent à partir d’une traduction algorithmique de propriétés issues du système visuel naturel. Cependant ces méthodes sont très restrictives et acquièrent toute leur performance dans des cas de figure bien précis, aucune des méthodes n’est universellement applicable.

Nous allons dans ce chapitre rappeler brièvement les méthodes dites classiques de traitement d’images. Nous étudierons ensuite des modèles plus complets de la rétine qui vont nous permettre de générer des algorithmes éprouvés, au sens biologique du terme, de traitement d’images.

1.7. MODELE EN TRAITEMENT D’IMAGE.

Les investigations en traitement d’image, pour la vision artificielle, se sont rapidement heurtées à la contradiction entre l’interprétation simple et rapide de scène pour les systèmes de vision naturelle et la quantité d’informations contenues dans une image échantillonnée. En effet, si nous présentons à un individu une scène de la vie courante, il n’aura aucune difficulté à reconnaître les différents objets qui la composent. Pourtant cette scène, étudiée en chaque point de l’image, représente une quantité d’information gigantesque.

Pour résoudre cette difficulté, il a fallu formaliser de manière scientifique le traitement visuel naturel et établir une théorie de la vision. Cette théorie a été résumée par Radu Horaud et Olivier Monga [22] de la manière suivante : « La vision est un processus de traitement de l’information. Elle utilise des stratégies bien définies afin d’atteindre ses buts. L’entrée d’un système de vision est constituée par une séquence d’images. Le système lui-même apporte un certain nombre de connaissances qui interviennent à tous les niveaux. »

David Marr [23] propose à la fin des années 70, un paradigme de la vision :

· La reconnaissance des contours des objets permet de les délimiter et de les structurer.

· L’accès à la troisième dimension se fait à partir d’images en deux dimensions ( appelées ébauche 2,5D) et des connaissances sur le monde 3D.

· L’extraction du relief à partir de l’ombre portée.

· La perception du mouvement dans des scènes animées.

David Marr fut le premier à rechercher une formalisation scientifique du problème de vision. Ses travaux ont permis d’engendrer un grand nombre d’application en donnant une formulation algorithmique aux différents points de son paradigme.

Une partie des traductions algorithmiques du paradigme de David Marr, qui a débouché sur des algorithmes efficaces, est organisée en trois étapes : segmentation, reconstruction, reconnaissance. Le but de la segmentation, est l’extraction d’attributs caractérisant les entités de l’image. C’est le traitement bas niveau de l’image.

Ce traitement bas niveau est défini de manière multiple, et consiste à donner une nouvelle représentation de l’image, un autre espace de représentation. Distinguons à ce point deux démarches particulières :

· La démarche classique de détection de contours, ou de régions ( filtrage gradient, laplacien, gaussien, deriche ) qui s’appuie sur des propriétés diverses, suivi par des algorithmes de segmentation en régions ( croissance de régions, agrégation de points ).

· La démarche de Yves Meyer [13], qui a effectué une relecture des travaux de David Marr sur les propriétés des cellules ganglionnaires. Ce dernier conjecture : « la représentation de base fournie par la rétine, est une succession d’épures effectuées à des échelles formant une progression géométrique. Ces épures sont faites de lignes et ces lignes sont les fameux zéro-crossing ». Ensuite Yves Meyer propose une formulation sous forme d’analyse en ondelettes, ou les lignes de zéro-crossing sont définies par la nullité des coefficients en ondelettes. Cette représentation à l’avantage d’être complète, donc de permettre la reconstruction du signal original.

Les différentes méthodes de traitement bas niveau, introduite précédemment, fournissent une nouvelle représentation de l’information contenue dans les images. A partir des caractéristiques mathématiques ou algorithmiques connues de ces représentations, il est possible d’appliquer des méthodes de plus haut niveau, pour réaliser les opérations de vision proprement dite. Dans notre démarche nous proposons une imitation plus détaillée de la structure biologique de la vision, avec comme limitation que nous ne connaissons pas de manière formelle détaillée, toutes les propriétés intrinsèques de l’espace de représentation ainsi engendré.

1.8. Modeles neuromimétiques.

Les modèles que nous allons présenter dans ce paragraphe, sont des imitations les plus détaillées possible de la structure neuronale mise en jeu dans la vision naturelle des vertébrés, d'où le terme neuromimétique. Cette démarche se fonde sur le « mythe » neuronal, à partir duquel est née toute une branche scientifique, les réseaux de neurones artificiels, qui sont au départ une imitation des réseaux de neurones naturels. La démarche scientifique est la suivante :

· Chercher une traduction algorithmique de la biologie, en utilisant des modèles des propriétés du traitement neuronal pour chaquun des neurones.

· Utiliser les outils mathématiques, en particulier le traitement du signal pour inférer sur le comportement global du réseau de neurones.

Nous allons tout d’abord détailler le modèle de neurones, puis nous expliquerons son application au modèle de rétine. Les différentes couches impliquées dans la rétine pour la detection du mouvement peuvent se représenter de la manière suivante :

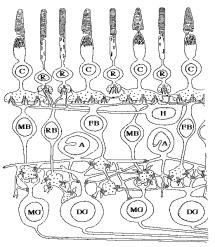
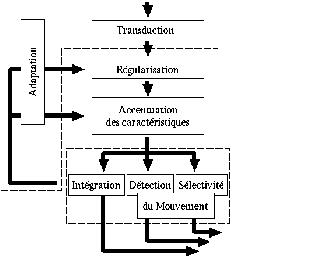
Figure 3. 14 : Schématisation du modèle de rétine W.Beaudot [11].

1.8.1 Modèle de neurones.

De nombreuses recherches ont été menées au laboratoire pour la modélisation des réseaux de neurones. Ces recherches ont permis de construire des réseaux de neurones artificiels applicables à des classes diverses de problèmes, séparation aveugle de sources, auto-organisation, l’analyse de données : Jeanny Herault et Christian Jutten [12]. Nous allons étudier dans ce paragraphe un modèle simplifié du neurone, ainsi que les différentes connexions synaptiques qui entrent en jeu dans les modèles biologiques de la rétine.

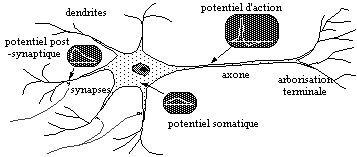
Figure 3. 15 : Motoneurone typique des vertébrés [12].

La transmission des signaux le long d’une dendrite peut se comparer à la transmission des signaux le long d’une paire de fils. C’est à dire caractérisé par un retard et un affaiblissement. Cette caractéristique est dûe à la membrane de la dendrite qui peut-être comparée à la mise en parallèle d’une capacité et d’une résistance de fuite.

Figure 3. 16 : Coupe d’une dendrite accompagnée de son modèle.

La réponse de la dendrite avec ce modèle est représentée sur la figure 3.4 et correspond à la relation suivante.

Pour les modèles de rétine, nous allons simplifier encore ce circuit, en considérant le système équivalent avec une seule résistance de fuite et une seule capacité de retard.

(a) (b)

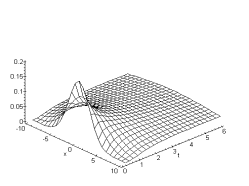
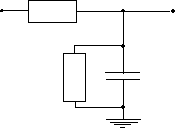
Figure 3. 17 : Modèle de transmission des signaux le long d’une dendrite.(a) Si la longueur x de la dendrite est courte la transmission est presque immédiate. Par contre lorsque la distance devient plus longue, le retard devient conséquent. (b) Modèle simplifié utilisé dans la suite.

Nous considérons plusieurs types de liaisons synaptiques pour les modèles de rétines, synapses chimiques, synapses composites, synapse réciproques, dont nous donnons la description électrique dans la figure suivante.

(a) (b) (c) (d)

Figure 3. 18 : Les quatre principaux types de connexions synaptiques suivi de leur modèle. (a) Synapse chimique (b) Synapse gap jonction (c) Synapse composite (d) Synapse réciproque.

1.8.2 Modèles de la PLE à un cône par cellules horizontales.

Les modèles de la rétine, développés par W.Beaudot et J.Hérault, ont comme point de départ le modèle de Mead. Carver Mead et son équipe de Caltech ont réalisé un circuit en silicium simulant les trois premières cellules de la rétine ( cellules photoréceptrices, horizontales et bipolaires ) [24]. La particularité de l’approche de Mead fut essentiellement d’intégrer un traitement temporel inséparable du traitement spatial. Leur modèle est fondé sur les principaux points suivant :

· Les photorécepteurs ont une réponse logarithmique, ce qui a pour effet de comprimer la grande dynamique de l’éclairage naturel.

· Les cellules horizontales forment un réseau dans lequel les signaux se propagent. Leur rôle est de réaliser une moyenne du signal de manière à former une référence à partir de laquelle le traitement aura lieu.

· Les cellules bipolaires ont un champ récepteur à antagonisme centre-périphérie. La partie centrale du champ récepteur est conforme à la réponse des photorécepteurs, alors que la partie périphérique correspond à l’influence locale du réseau de cellules horizontales.

Le modèle électronique proposé par Mead est le suivant (figure 3.6). Il correspond au modèle de transmission le long d’une dendrite (en omettant la résistance de fuite membranaire), une connexion gap-jonction entre les cellules horizontales et deux liaisons synaptiques chimiques de signes opposés entre les cellules bipolaires, horizontales et les récepteurs.

(a) (b)

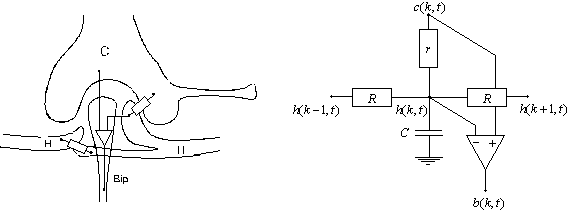
Figure 3. 19 : Modèle de la rétine de Mead. (a) Représentation de la triade synaptique (b) Son équivallent électrique pour le modèle de Mead.

1.8.2.1 Modèle .

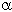Les modèles de réseaux de neurones que nous avons exposés plus haut permettent d’enrichir le modèle de Mead. C’est le travail qu’ont effectué J.Hérault et W.Beaudot [14]. La première extension qu’ils proposèrent fut d’ajouter une résistance de fuite en parallèle avec la capacité C. Cette résistance est conforme au modèle de transmission des signaux le long d’une dendrite que nous avons précisé plus haut.

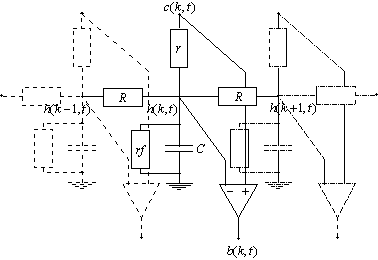
Figure 3. 20 : Première extension de la rétine de Mead. Modèle de la rétine de W.Beaudot et J.Hérault.

A partir de la loi des noeuds appliquée au noeud , nous pouvons exprimer l’évolution de la tension à travers le réseau de résistances équivalent au réseau de cellules horizontales.

(3.2.1)

Nous pouvons réécrire cette relation en multipliant tous les membres par et en posant , et de la manière suivante :

(3.2.2)

En appliquant la transformée de Fourier à la variable continue , et la transformée en Z à la variable discrète , nous obtenons la fonction de transfert correspondant au réseau des cellules horizontales. La différence avec le modèle de Mead réside dans le paramètre ( pour le modèle de Mead). Appelons la transformée de Fourier et la transformée en Z de suivant et , et la transformée de Fourier et la transformée en Z du signal d’entrée . Nous écrivons la fonction de transfert du réseau des cellules horizontales de la manière suivante :

(3.2.3)

Pour étudier le comportement fréquentiel de cette fonction de transfert, il suffit de considérer la transformée de Fourier d’une variable discrète comme la substitution de dans la transformée en Z. La discrétisation de la variable à alors pour effet de rendre périodique le spectre avec pour période . La fonction de transfert devient :

(3.2.4)

La première remarque concernant cette fonction de transfert est son inséparabilité spatio-temporelle, c’est à dire que le traitement spatial ne peut-être séparé du traitement temporel. Nous pouvons également remarquer le comportement passe-bas, aussi bien pour les fréquences spatiales que pour les fréquences temporelles.

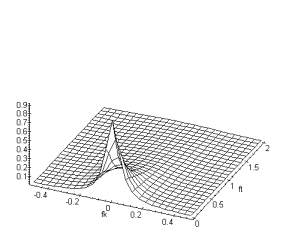
Figure 3. 21 : Représentation du module de la fonction de transfert de la couche des cellules horizontales du modèle de W.Beaudot et J.Herault. ()

Le comportement passe-bas de la couche des cellules horizontales lui confère un rôle de référentiel. En effet le réseau des cellules horizontales correspond à une moyenne spatio-temporelle du signal provenant des cônes.

Le traitement effectué par les cellules bipolaires s’écrit de la manière suivante :

(3.2.5)

En appliquant le même calcul que pour le réseau des cellules horizontales, et en appelant la transformée de Fourier bidimensionnelle de suivant les variables et , nous obtenons comme fonction de transfert des cellules bipolaires :

(3.2.6)

La fonction de transfert totale du modèle , , est donc une différence entre le signal des cônes, et sa version filtrée passe-bas par les cellules horizontales. Cette différence implique pour le modèle complet un filtrage passe-haut spatio-temporel.

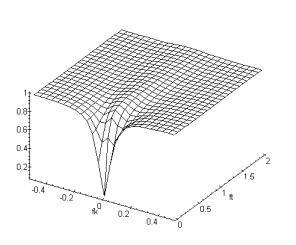
Figure 3. 22 : Module de la fonction de transfert totale du modèle de W.Beaudot et J.Herault. ().

Le filtrage passe-haut spatio-temporel confère à notre modèle des propriétés de rehaussement de contours au niveau spatial, et une accentuation d’objets en mouvement au niveau temporel [11]. En effet, le filtrage passe-haut peut-être considéré comme une différence entre deux échantillons consécutifs, autrement dit, le filtre [+1 -1] est passe-haut. Il est alors évident que la différence entre deux échantillons consécutifs sur une image sera nulle pour deux échantillons égaux, alors qu’elle sera grande pour deux échantillons opposés. Il en est de même pour deux points de deux images consécutives dans le temps.

Les paramètres sont appelés paramètres fonctionnels du modèle, alors que les paramètres , sont appelés paramètres structurels de la rétine biologique. Avant de présenter les autres extensions du modèle de Mead, nous allons détailler l’influence des paramètres fonctionnels du modèle. Les extensions suivantes comportent des paramètres fonctionnels jouant le même rôle que dans la première extension.

En reprenant l’équation (3.2.4) du filtrage passe-bas de la couche des cellules horizontales, et en posant et , la fonction de transfert s’écrit également :

(3.2.7)

Ce qui signifie en représentation asymptotique :

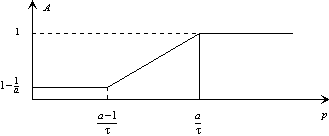
Figure 3. 23 : Représentation de l’influence des paramètres fonctionnels du modèle sur le module de la fonction de transfert.

Nous remarquons que les paramètres sont responsables du niveau de coupure en basse-fréquences, ainsi que de l’emplacement de la fréquence de coupure. Remarquons également qu’il n’y a qu’un degré de liberté, c’est à dire que la fréquence de coupure et le gain en basse fréquence dépendent des mêmes paramètres. Constatons cependant que la variation possible des paramètres du modèle permet de conserver une variabilité des algorithmes.

1.8.2.2 Modèle .

Pour le modèle suivant, nous considérons que les cellules réceptrices sont également connectées en réseau à travers des liaisons gap-jonction, et que les signaux subissent un retard et un affaiblissement en se propageant le long des dendrites des récepteurs.

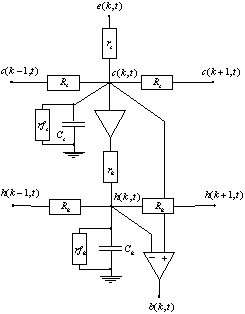
Figure 3. 24 : Modèle de la PLE.

La fonction de transfert de ce filtre peut se calculer aisément à partir de la fonction de transfert du modèle précédent. En effet le filtrage passe-bas réalisé par la couche des photorécepteurs est équivalent de celui réalisé par les cellules horizontales, aux valeurs des paramètres structurels près. De plus les fonctions de transfert sont découplées par l’amplificateur opérationnel séparant les deux couches. Il suit de cette remarque, et en posant , l’équation de la fonction de transfert de chaque couche du modèle .

Le signal résultant des bipolaires se déduit par la structure de la triade synaptique :

Figure 3. 25: Diagramme de calcul des signaux dans la triade synaptique. Les bipolaires effectuent une différence entre le signal filtré par la couche des cônes et le même signal refiltré par la couche des cellules horizontales.

Nous en déduisons la fonction de transfert entre les cellules bipolaires et l’entrée :

(3.2.8)

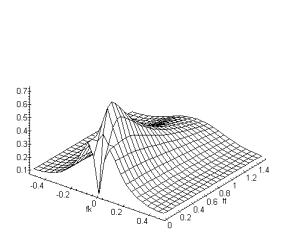
Figure 3. 26 : Module de la fonction de transfert du modèle de la PLE. ()

La fonction de transfert est maintenant passe-bande spatio-temporelle. Le filtrage passe-bas de la couche des cônes, réalise un lissage de l’image d’entrée, le traitement correspondant permettra une réduction du bruit. Il est important de constater que le changement affecte le traitement spatial et le traitement temporel, il s’agit d’une régularisation spatio-temporelle [11].

1.8.2.3 Modèle .

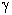La dernière extension du modèle de la PLE qu’ont proposés J.Hérault et W.Beaudot prend en considération la rétroaction des cellules horizontales sur les photorécepteurs. C’est à dire qu’on suppose qu’il y a une connexion synapse réciproque entre les deux premières couches de la PLE.

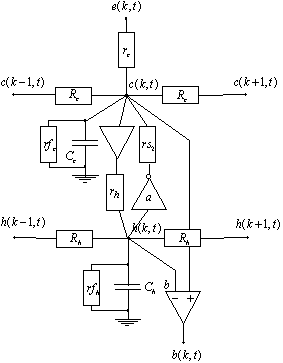
Figure 3. 27 : Modèle de la PLE. Utilisation d’une synapse réciproque entre la couche des cônes et celle des cellules horizontales.

Pour déterminer la fonction de transfert du système, il faut calculer la tension et l’impédance équivalente, au point , à la superposition de la source de tension fournie par et le retour depuis . La tension équivalente est appelée et la résistance équivalente . Soit en appelant nous obtenons pour fonction de transfert de la couche des cônes :

(3.2.9)

Soit en appelant , , , et , nous obtenons :

Finalement :

(3.2.10)

Figure 3. 28 : Fonction de transfert du modèle . ()

William Beaudot qualifie à juste titre ce modèle par les deux termes suivant : augmentation de la sensibilité et de la sélectivité. Ces qualificatifs sont repérables sur la forme de la fonction de transfert, et peuvent également se justifier par le phénomène de rétroaction bien connue des électroniciens ( système bouclé ).

En reprenant l’équation (3.2.10) et en supposant d’ordre 0 et d’ordre 1 pour simplifier le discours[C1] [4], on peut écrire :

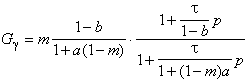(3.2.11)

Nous remarquons sur la figure suivante que les paramètres a et b confèrent deux degrés de libertés, au module de la fonction de transfert simplifiée.

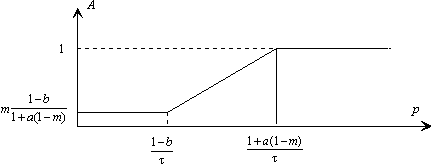
Figure 3. 29 : Influence des paramètres a et b sur le module de la fonction de transfert simplifiée.

1.8.3 Modèle de la PLE à deux cônes par cellules horizontales.

Nous avons également développé un modèle à deux connexions de cônes par cellules horizontales. La raison est d’ordre biologique, en effet il semble que cette architecture soit plus réaliste. La représentation schématique en biologie de la triade synaptique fait intervenir une connexion entre chaque cellule réceptrice et deux cellules horizontales dont les dendrites s’étendent de chaque coté de la cellule réceptrice. Nous avons représenté sur la figure suivante le schéma général de ce nouveau modèle avec une couche pour les cônes et une couche pour les cellules horizontales[5].

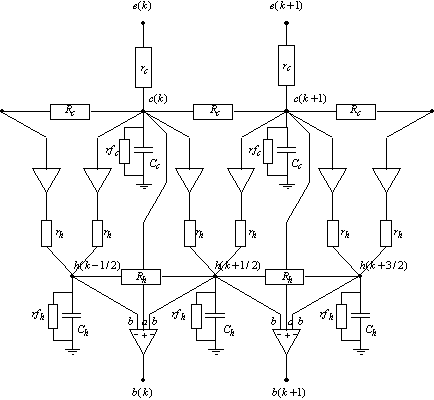
Figure 3. 30 : Modèle de la rétine à deux cônes par cellules horizontales.

La fonction de transfert de la couche des cônes reste inchangée, c’est à dire que nous avons pour fonction de transfert . Cependant la fonction de transfert entre les cellules horizontales et les cônes est entièrement modifiée. Nous avons par la loi des noeuds appliquée au noeud :

(3.2.12)

La fonction de transfert s’obtient par des calculs similaires que pour obtenir la relation (3.2.3), et s’écrit :

(3.2.13)

La relation liant les bipolaires aux autres cellules est la suivante :

(3.2.14)

Soit la fonction de transfert totale est la suivante :

(3.2.15)

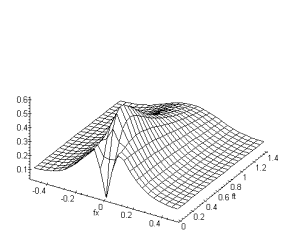
Figure 3. 31 : Module de la fonction de transfert du modèle . ()

L’essentiel de la modification de la fonction de transfert pour ce nouveau modèle, se caractérise par un gain spatial légèrement plus élevé en basse fréquences temporelles. En effet le filtrage passe-bas des cellules horizontales est modulé par une fonction qui a pour effet d’atténuer le gain passe-bas du filtrage des cellules horizontales. Cette atténuation à pour effet d’augmenter le gain passe-bande de la fonction de transfert totale pour les basses fréquences temporelles.

1.9. Perception ‘coarse TO FINe’

Le filtrage spatio-temporel réalisé par les modèles de rétine est de type passe-bande et à variables non séparables. La proprièté qui résulte de cette inséparabilité est une dépendance temporelle de la fonction de transfert spatiale. La figure suivante représente l’évolution de la fonction de transfert spatiale en fonction du temps pour un échelon unité temporel. Pour obtenir cette courbe nous avons calculé la réponse temporelle indicielle de la fonction de transfert. Cette réponse correspond à la présentation d’une stimulation constante à l’entrée du modèle de rétine. Nous remarquons (figure 3.19) une différence de comportement entre les basses fréquences spatiales et les hautes fréquences spatiales au cours du temps. Lorsqu’on présente une image en entrée du système, la sortie est le résultat d’un filtrage spatial d’abord passe-bas avec une fréquence de coupure élevée qui évolue au cours du temps vers un filtrage passe-bande.

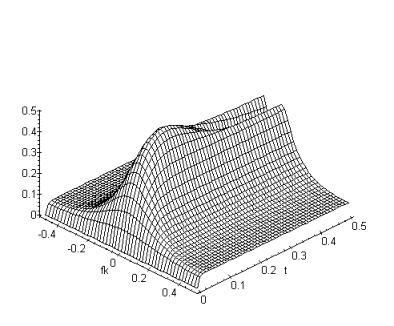
Figure 3. 32 : Représentation de l’évolution de la fonction de transfert spatiale en fonction du temps, pour un échelon unité temporel. Nous voyons une prédominance des basses fréquences spatiales, qui finalement laisse place aux hautes fréquences spatiales.

Afin de différencier la perception des hautes et des basses fréquences spatiales, une nouvelle méthode expérimentale à été mise au point au laboratoire par Aude Oliva [15]. Cette méthode consiste en la création d’images dites hybrides : Les basses fréquences spatiales d’une image sont mélangées aux hautes fréquences spatiales d’une autre image. Ces hybrides ont été présentés à des sujets pour des durées variables (30,50 et 100 ms). A partir de la réaction des sujets, on observe qu’au début du traitement visuel (<30ms) les basses fréquences spatiales sont perçues avant les hautes fréquences spatiales et après (>30ms) les hautes fréquences spatiales dominent la réponse. Ce protocole expérimental, en quantifiant les temps de reconnaissance d’images a également permis d’estimer une plage de valeurs pour les paramètres de notre modèle.

Nous avons également remarqué, avec le modèle de rétine, que lorsque la stimulation est coupée, les hautes fréquences spatiales retombent très rapidement. Inversement les basses fréquences spatiales vont reparaitre sous forme d’un rebond relativement long (non représenté).

Chapitre 4 :

Application des modeles de retine a la vision en couleur.

Nous avons adapté les modèles de rétines du chapitre précédent à la vision chromatique. La particularité du traitement chromatique réside dans le fait que nous considérons la répartition des récepteurs sur un maillage hexagonal. Cette particularité est fondée biologiquement [25] et elle permet au niveau du traitement d’images d’avoir une répartition homogène des trois types de récepteurs rouge, vert et bleu.

Nous allons étudier dans ce chapitre les propriétés fréquentielles induites par l’échantillon-nage hexagonal. Puis nous verrons l’application des modèles de rétines étudiés précédemment, sur le maillage hexagonal. Enfin nous verrons les différentes interprétations possibles de ces calculs, ainsi que leurs conséquences sur le traitement d’images couleur et sur la vision naturelle.

1.10. Echantillonnage hexagonal.

Le maillage hexagonal confère des propriètées particulières à l’échantillonnage. Certaines de ces propriètés sont utilisées en traitement d’image pour simplifier l’application d’opérateurs de traitement. Par exemple le suivi de contours qui exploite la dualité entre la 4 connexité et 8 connexité sur le maillage hexagonal. Nous allons détailler dans ce paragraphe les conséquences de l’échantillonnage hexagonal pour la représentation spectrale.

Nous avons représenté sur la figure suivante l’opération d’échantillonnage d’une image continue en une image discrète sur maillage hexagonal.

Figure 4. 33 : Opération d’échantillonnage hexagonal d’une image continue. représente l’image continue, représente le peigne de Dirac en deux dimention sur maillage hexagonal et l’image échantillonnée. L’échantillonnage est effectué par multiplication de l’image continue par le peigne de Dirac.

Le peigne de Dirac est défini par la relation suivante :

(4.1.1)

Nous présentons sur la figure suivante la convention qui à été adoptée pour la formulation du peigne de Dirac sur un maillage hexagonal.

Figure 4. 34 : Paramétrisation de l’espace pour le peigne de Dirac sur maillage hexagonal.

Nous pouvons considérer ce peigne de Dirac comme la somme de deux peignes sur deux maillages rectangulaires décalés, en décomposant la somme pour les valeurs de j paires et les valeurs de j impaires.

(4.1.2)

Les deux peignes et sont périodiques de période en et en y sur maillage rectangulaire, et on peut les décomposer en serie de Fourier.

avec

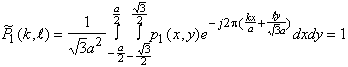
Par suite la transformée de Fourier de s’écrit :

soit

(4.1.3)

De la même manière, nous pouvons écrire pour :

avec

or est non nul pour et sur l’intervalle bidimentionnel considéré, soit :

Soit

La transformée de Fourier s’écrit alors :

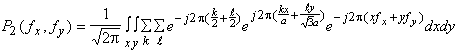
soit :

(4.1.4)

Finalement à partir de (4.1.3) et (4.1.4) et en assemblant les termes de la somme :

Or , soit un terme sur deux s’annule alternativement.

Nous pouvons donc exprimer le résultat précédent sous forme condensée :

(4.1.5)

Finalement la transformée de Fourier du signal est donné par la relation suivante :

(4.1.6)

La convolution par le peigne de Dirac à pour effet de rendre le spectre périodique. La structure hexagonale en fréquences est tournée d’un quart de tour.

Figure 4. 35 : Représentation de la périodicité de la structure duale en fréquence pour une structure spatiale hexagonale.

La periodicité en fréquence implique des conditions sur l’échantillonnage pour éviter le repliement du spectre. Notons que le plus petit pas d’échantillonnage entre et se trouve le long de l’axe , ou celui-ci vaut , alors que la plus petite période entre et est pour et vaut . Il suit que pour la fréquence d’échantillonnage donnée , la fréquence maximale du signal pour laquelle il n’y a pas de repliement de spectre est .

1.11. MOdeles sur maillage hexagonal.

1.11.1 Modèle pour la couleur.

1.11.1.1 Modèles à une connexion entre cônes et cellules horizontales.

L’application des modèles de rétine pour la vision en couleur se fait en écrivant la fonction de transfert sur une architecture hexagonale, en considérant un seul type de récepteur par pixel. Le schéma suivant représente l’architecture des connexions entre cellules horizontales et cônes. Les deux couches de cellules se superposent, et en un point donné chaque recepteur est connecté avec la cellule horizontale de dessous. Chacune des cellules réceptrices et horizontales sont ensuite connectées sur les cellules bipolaires de dessous. Cette architecture respecte entièrement la formation en triade synaptique du modèle du chapitre 3, la différence réside dans les connexions entre cellules de même type sur une même couche. La particularité de l’architecture est un maillage monochromatique des cônes, alors que le maillage des cellules horizontales est polychromatique.

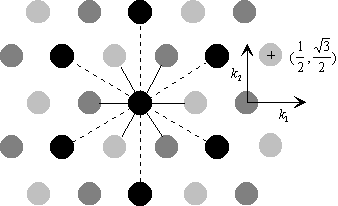
Figure 4. 36 : Représentation de l’architecture des cellules réceptrices et horizontales en vue de dessus.Les différents niveaux de gris représentent les différents types de récepteurs (rouge, vert et bleu). Les deux couches sont superposées, et à chaque récepteur correspond une cellule horizontale, ainsi qu’une cellule bipolaire. Les récepteurs sont connectés en polychromie ( traits continus) alors que les cellules horizontales sont connectées en monochromie (traits pointillés).

Nous pouvons considérer les connexions des cônes en monochromie comme un sous-échantillonnage. Appelons un signal fictif échantilloné sur un maillage hexagonal, avec trois couleurs par pixel. peut s’écrire comme suit :

(4.2.1)

Où représentent les trois signaux correspondant aux trois plans de couleurs rouge, vert et bleu. Le signal à l’entrée de la couche des cônes peut s’écrire de la manière suivante.

avec :

(4.2.2)

Les fonctions sont des fonctions de sous échantillonnage de un point sur trois sur maillage hexagonal. Nous les avons représenté sur la figure suivante en vue de dessus et en coupe pour .

(a) (b) (c)

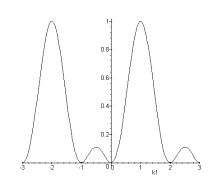
Figure 4. 37 : Fonction de sous échantillonnage en vue de dessus et en coupe pour (a) les couleurs rouges (b) les couleurs vertes (c) les couleurs bleues

Nous pouvons alors écrire :

(4.2.3)

Où le premier terme de cette somme représente la luminance du signal et les trois autres termes les chrominances modulées rouge, verte et bleu du signal. La transformée de Fourier peut s’écrire comme suit en posant R, V, B, E les transformées de Fourier de r, v, b, e et .

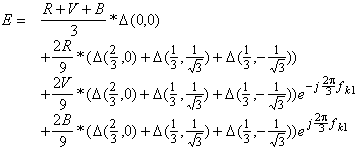(4.2.4)

Nous retrouvons dans cette dernière relation la période hexagonale du spectre conformément à la relation (4.1.6). Cependant nous remarquons que le spectre de la partie luminance du signal se trouve en bases fréquences, alors que celui des différentes chrominances se trouve en plus hautes fréquences. Nous avons représenter cette proprièté du sous-échantillonnage couleur sur la figure suivante.

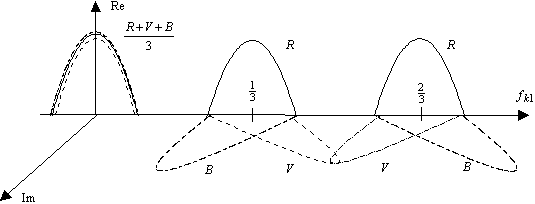
Figure 4. 38 : Effet du sous échantillonnage sur la fonction de transfert du signal d’entrée.

Cette particularité du spectre du signal sous-échantillonné va nous permettre de comprendre les propriètés du filtrage rétinien sur maillage hexagonal. La figure suivante montre le détail des connexions horizontales et verticales pour la couche des cellules réceptrices[6].

Figure 4. 39 : Connexions mises en jeu pour la couche des cellules réceptrices. Attention les axes ont été tournés d’un quart de tour dans le sens trigonomètrique.

A partir de la loi des noeuds sur on a :

avec

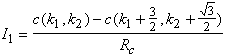
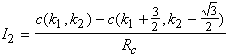
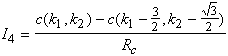
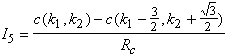
En regroupant les termes nous obtenons comme équation générale du système :

(4.2.5)

Soit en posant , et :

(4.2.6)

Comme pour le chapitre 3, nous appliquons la transformée en Z suivant les variables et et la transformée de Fourier suivant la variable temporelle. Nous obtenons la fonction de transfert de la couche des cellules réceptrices sur un maillage hexagonal.

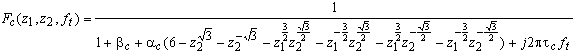(4.2.7)

Soit en substituant et nous obtenons la transformée de Fourier discrète.

(4.2.8)

Nous avons représenté le module de la fonction de transfert pour les variables fréquence spatiale-fréquence temporelle () et fréquence spatiale-fréquence spatiale ().

(a) (b)

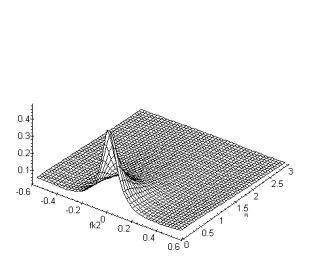
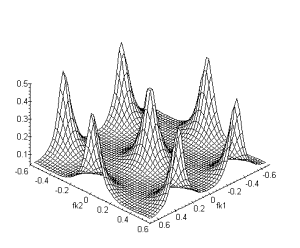
Figure 4. 40 :Nature passe-bas spatio-temporelle de la couche des cônes (a) Module de la fonction de transfert fk2 et ft. (b) Fonction de transfert fk1, fk2. La périodicité du spectre est sur l’intervalle ().

Nous avons également représenté la structure hexagonale des connexions entre les cellules horizontales :

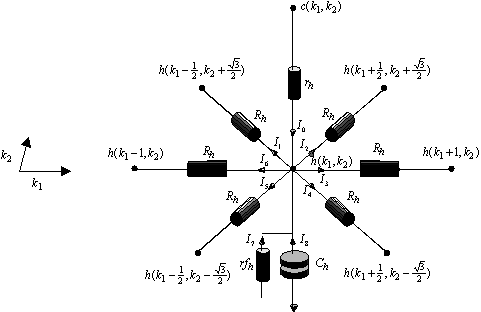
Figure 4. 41 : Connexion mise en jeu pour la couche des cellules horizontales.

Par les mêmes techniques de calcul que précédement, nous obtenons pour fonction de transfert: (4.2.9)

(a) (b)

Figure 4. 42 : Nature passe-bas spatio-temporelle de la couche des cellules horizontales. (a) Module de la fonction de transfert pour fk1, ft. (b) Fonction de transfert fk1,fk2. La périodicité du spectre est cette fois-ci sur l’intervale . ()

La fonction de transfert globale s’écrit :

(4.2.10)

(a) (b)

Figure 4. 43: Comportement fréquentiel à la sortie des bipolaires. (a) Module de la fonction de transfert fk1, ft. (b) Fonction de transfert fk1,fk2. La différence de périodicité des fonctions de transfert entre la couche des cônes et celle des cellules horizontales implique deux modes de fonctionnement différent en basses et en hautes fréquences spatiales.

Remarquons pour cette dernière figure que les différences de périodicité des fonctions de transfert de la couche des cônes et celle des cellules horizontales impliquent deux modes de fonctionnement au système global. Un fonctionnement passe-bande spatio-temporel pour les basses fréquences spatiales, et un fonctionement passe-bas spatio-temporel modulé pour les hautes fréquences spatiales. En se reportant à la représentation du spectre (figure 4.6) établie précédement, nous remarquons que le mode de fonctionnement en basses fréquences correspond au traitement de la luminance, alors que celui des hautes fréquences spatiales correspond à la chrominance.

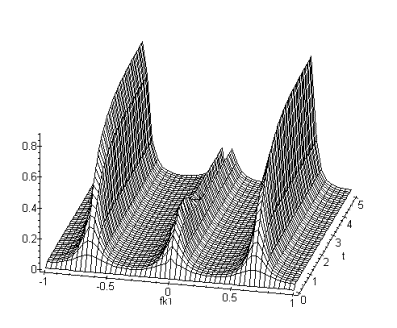
Figure 4. 44 : Réponse temporelle à un échelon unité du modèle sur maillage hexagonal.

La réponse temporelle à un échelon unité du modèle sur maillage hexagonal fait apparaitre une dominance des signaux de couleur par rapport à ceux de luminance. Les signaux de couleur se positionnent rapidement à leur régime dominant. La luminance au contraire met beaucoup plus de temps à se stabiliser. Elle fait apparaitre une prédominance des basses fréquences spatiales, qui s’estompe ensuite pour laisser place au régime des hautes fréquences. Ces remarques laissent présager que lorsque l’on ouvre les yeux apparait tout d’abord des informations de luminance et de couleur qui donnent un rendu globale de la scène. Ensuite au fur et mesure que les informations de couleur se stabilise, la luminance vient coder les informations de détail.

Les propriètés des différents modèles que nous avons présenté dans le chapitre 3 seront respectées sur maillage hexagonal. En tenant compte que les deux modes de fonctionnement (HF et BF spatiale) sont induit de manière différente par chacune des couches de la rétine. Le mode passe-bande des basse-fréquences spatiales (luminance) est issu de la différence entre la fonction de transfert des cônes et la fonction de transfert des bipolaires, alors que le mode passe-bas modulé des hautes fréquences spatiales (chrominance) résulte uniquement de la couche des cellules réceptrices.

1.11.1.2 Modèles à sept cônes par cellules horizontales.

Nous avons également cherché à transposer le modèle à deux cônes par cellules horizontales sur maillage hexagonal. Considérons qu’à chaque récepteur correspond une cellule horizontale et une cellule bipolaire conformement à la triade synaptique. Les recepteurs et les cellules horizontales sont connectées entre eux de la même manière que pour la figure 4.4, c’est à dire les recepteurs sont en monochromie et les cellules horizontales en polychromie. Par contre chaque cellule horizontale reçoit 7 connexions synaptiques provenant de la cellule réceptrice du dessus et des 6 cellules receptrices voisines.

La fonction de transfert des cellules réceptrices n’est pas modifiée, par contre nous pouvons écrire pour la fonction de transfert des cellules horizontales :

(4.2.11)

(a) (b)

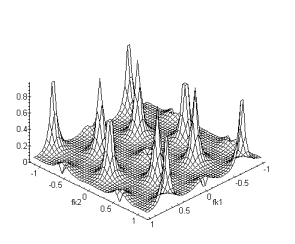
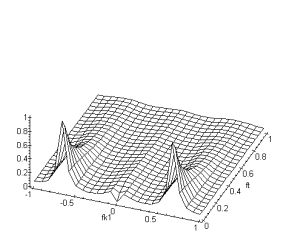
Figure 4. 45 : (a) Fonction de transfert spatial globale du modèle à sept cônes par cellules horizontales. (b) Module de la fonction de transfert spatio-temporelle.

Nous remarquons que, pour des paramètres adaptés, la fonction de transfert du modèle à septs cônes par cellules horizontales n’est pas différente de la fonction de transfert à un cône par cellules horizontales. Le profil général n’est pas modifié est cela confirme la validité des modèles précédents. Par contre les temps de calculs correspondant sont plus faible pour les anciens modèles que pour celui-ci.

Nous avons également envisagé de construire d’autres types d’architectures sur maillage hexagonal, pour tenir compte de la proportion des cellules dans la rétine.

Figure 4. 46 : Architecture possèdant une plus grande proportion de cellules horizontales que de récepteurs et de bipolaires. Les cellules bipolaires sont disposées au dessous de chaque récepteur.

Avec d’autres types de constructions il est également possible de varier la proportion différemment. On peut également construire une architecture qui possède des cellules horizontales connectées à des types de cônes particulier (R-V, V-B et B-R). Ceci afin de modéliser les cellules horizontales spécialisées à certaines couleurs.

Ces variantes du modèle de base offrent la possibilité d’une modélisation plus globale de la rétine. En tenant compte de l’architecture naturelle, décrite dans différents articles de biologie, il est possible de décrire un modèle variable en fonction de la position considérée dans la rétine.

Cette globalisation semble indispensable pour tenir compte de certains phénomènes :

· Apparition de couleur bleu au centre du champ visuel alors que la fovéa centrale est démunie de récepteurs bleus.

· Echantilonnage variable des photorécpteurs suivant l’excentricité dans la rétine.

· Projections rétino-corticales variables.

Nous n’avons pas eu le temps de travailler davantage cette partie. Nous pensons que la première étape de cette construction passe par un examen minutieux des articles de biologie au sujet de la structure rétiniene, pour obtenir un modèle détaillé de son architecture.

1.11.2 Opposition de couleurs.

Nous avons vu précédement que le sous échantillonnage de un sur trois du signal de couleur d’origine à pour effet de coder différemment les signaux de chrominance de la luminance. Nous avons également étudié la fonction de transfert du filtrage rétinien, qui ne modifie pas la position de la luminance et de la chrominance en fréquence spatiale mais qui les module dans le temps. Voyons maintenant ce que contiennent les canaux de luminance et de chrominance.

Pour séparer dans le spectre fréquentiel les canaux de chrominance et de luminance, nous avons défini le filtre de démodulation suivant :

(4.2.12)

Ce filtre s’applique sur le signal de la manière suivante :

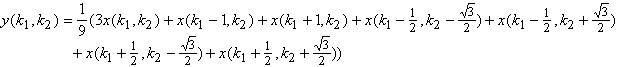
C’est à dire qu’il correspond au noyau [1 3 1] appliqué sur maillage hexagonal. La figure suivante représente le filtre défini, et son effet sur la fonction de transfert de la figure 4.11 (b).

(a) (b)

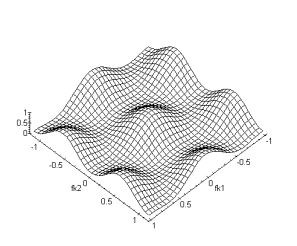
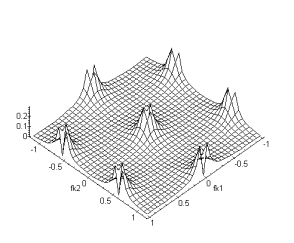
(c) (d)

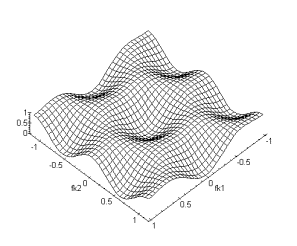
Figure 4. 47 : Effet de la fonction de séparation de luminance et chrominance sur le spectre de la fonction de transfert. (a) Fonction de démodulation de luminance d. (b) Application sur le spectre. Seule la luminance est conservée. (c) Fonction de démodulation de chrominance (1-d) (d) Effet sur le spectre.

Pour obtenir les chrominances, il suffit d’appliquer le filtre sur le spectre de la fonction de transfert. Ce calcul est équivalent à soustraire le spectre de luminance au spectre complet de la fonction de transfert.

D’après la relation (4.2.3) les signaux de chrominance après le filtrage de séparation sont donnés par la relation suivante :

Nous avons pu vérifier, à l’aide du logiciel Maple, qu’en multipliant ce signal ch par les fonctions de sous échantillonnage définies précédemment, nous obtenons :

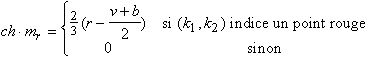
(4.2.13)

C’est à dire qu’en démodulant les composantes de la chrominance, par les mêmes fonctions qu’à la modulation, nous obtenons en position des points rouges, l’opposition de couleur rouge-cyan, en position des points verts, l’opposition vert-magenta et en position des points bleus, l’opposition bleu-jaune. Si nous appliquons les mêmes transformations aux signaux issus du filtrage rétinien, nous retrouvons également ces différents canaux. Cependant le filtrage rétinien vient moduler ces canaux en fonction du temps.

Le simulateur que nous avons construit permet de mieux se rendre compte des conséquences du filtrage de la rétine sur les canaux d’opposition de couleur et de luminance. Nous ne pouvons malheureusement pas insérer d’images sortie du simulateur, car celle-ci sont d’un rendu médiocre en noir et blanc.

Cependant nous allons commenter une expérience réalisée par le simulateur. Nous présentons pour cette expérience un film constitué de 20 images. Les dix premières contiennent un carré rouge sur fond noir. Les dix suivantes sont complètement noir. Le traitement rétinien pour cette expérience consiste à calculer les images à la sortie des bipolaires, puis à les filtrer pour en tirer les canaux d’opposition de couleurs et de luminance. Nous avons également intégré un algorithme qui reconstruit les scènes à partir des canaux d’opposition de couleur et de luminance. Après le traitement rétinien, il apparait à partir de la cinquième image, dans l’image reconstruite, un halo cyan autour du carré rouge. Puis à partir de la dixième image nous avons remarqué le phénomène de désaturation. C’est à dire qu’il apparait dans la scène l’image du carré en opposition de couleur, qui s’efface au cours du temps.

Nous avons également remarqué le comportement du filtrage temporel au cours du temps conformement à la figure 4.12. C’est à dire que lorsque l’image apparait, les informations de couleur et de luminance passe bas se présentent, puis lorsque la couleur est stabilisée, il apparait des détails de luminance.

1.12. modele de v1.

Dans cette partie, nous supposons que l’aire V1 reçoit les canaux d’opposition de couleurs issus de la rétine. Nous allons proposer un modèle de V1 pour l’effet McCollough, à partir des canaux d’opposition de couleur et de l’algorithme de séparation de sources.

Le séparation de sources est une méthode basée sur les réseaux de neurones artificiels. Elle permet de réaliser une analyse en composante indépendante sur des vecteurs.

Nous disposons d’un observable à N dimensions, qui est issu du mélange linéaire A de M sources . Le mélange et les sources sont inconnues. En émettant les hypothèses suivantes nous allons séparer de l’observable les différentes sources.

·La dimension de l’observable est égale au nombre de sources, M=N.

·La matrice de mélange A est de rang M.

·Les sources sont statistiquement indépendantes.

La solution de ce problème est donnée par un réseau de neurones artificiels à connections inhibitrices récurrentes. Sans entrer dans les détails, on démontre que pour obtenir des sorties statistiquement indépendantes, il convient d’adopter une règle d’apprentissage des moments. Par exemple la règle suivante des moments croisés d’ordre 4 donne de bons résultats pour des signaux sous-gaussiens.

La matrice des coefficients C du réseau, si l’apprentissage converge, représente la matrice de mélange A à une matrice de permutation près.

Nous avons appliqué cet algorithme à l’effet McCollough. La phase d’apprentissage consiste à présenter au réseau un vecteur à trois composantes : opposition de couleur rouge-cyan, opposition de couleur vert-magenta, orientation. Les couleurs rouge-cyan et vert-magenta et l’orientation peuvent valoir 1, 0, ou -1. Parmi l’ensemble des vecteurs possibles avec cette représentation, nous avons choisi de présenter au réseau l’ensemble des vecteurs suivants :

VECTEURS D’ADAPTATION	rouge orientation verticale	vert orientation horizontale	noir sans orientation	blanc sans orientation
rouge-cyan	1	0	0	1
vert-magenta	0	1	0	1
orientation	1	-1	0	0

Nous disposons au laboratoire d’un simulateur de réseau pour la séparation de sources. Après quelques adaptations de ce dernier, nous avons réalisé l’apprentissage avec les vecteurs décrits dans le tableau précédents. Le réseau utilisé dans ce cas comporte 3 neurones, car nous disposons d’une entrée en dimension 3 :

Figure 4. 48 : Réseau de séparation de sources à trois neurones pour l’effet McCollough.

A la fin de l’apprentissage les coefficients ont convergé. La valeur des coefficients à ce moment est tel que les signaux de sortie S1, S2, S3 sont décoréllés. Nous présentons les vecteurs de tests suivants au réseau de neurones et notons les sorties du réseau.

VECTEURS DE TEST	blanc orientation verticale	blanc orientation horizontale	SORTIE DU TEST	cyan+vert même orientation	magenta+rouge même orientation
rouge-cyan	1	1	S1	-1.25	0.25
vert-magenta	1	1	S2	0.25	-1.25
orientation	1	-1	S3	0.75	-0.75

Nous avons remarqué que les sorties du réseau sont conformes à ce que nous avons observé lors de l’induction par l’effet McCollough. La phase d’apprentissage du réseau correspond à l’induction de celui-ci par l’effet. La phase de test correspond à l’apparition de fausses couleurs contrainte par l’orientation.

Le vraisemblance des résultats de simulation obtenus par rapport à la réalité laisse supposer qu’une partie des cellules de l’aire V1 agissent comme des séparateurs de sources entre les canaux d’opposition de couleurs et l’orientation.

chapitre 5 :

implantation du simulateur.

Le passage d’un algorithme sous forme symbolique à son implentation sur machine n’est pas toujours aisé. La première partie de ce chapitre y est entièrement consacrée. Les problèmes concernent essentiellement la représentation du maillage hexagonal en mémoire interne, et l’approximation temporelle de la fonction de transfert. Le deuxième partie de ce chapitre est un descriptif du simulateur.

1.13. Conversion maillage carre vers mailLage hexagonal.

Les images couleurs que nous traitons habituellement sont sur un maillage carré avec trois couleurs par pixel. Ce format est celui que donnent les systèmes d’acquisition en couleur. Comme nous l’avons étudié dans le chapitre précédent, les images traitées par notre modèle de rétine sont sur maillage hexagonal avec un seul type de couleur par pixel. Il faut donc réaliser une conversion de maillage pour traiter les images du système d’acquisition (caméra) avec le modèle de rétine.

Figure 5. 49 : Type de conversion imposé par le traitement rétinien. Il faut changer 3 plans monochromatiques sur maillage carré en un plan trichromatique sur maillage hexagonal.

Nous avons tout d’abord choisi la taille du maillage hexagonal en imposant des critères de conversions. Parmi tous les critères possibles nous avons sélectionné les suivants :

· Conserver le même nombre de pixel en horizontal et vertical pour éviter les déformations géométriques de l’image.

· Réduire au minimum les calculs pour la conversion, en effectuant une interpolation dans une seule direction.

· Conserver la même quantité d’information pour respecter le théorème de Shannon.

Le troisième critère est indispensable en traitement d’image, cependant nous avons opté pour le deuxième. Le premier cumule les inconvénients de l’un et de l’autre critère et nous l’avons rapidement abandonné.

Le choix que nous avons effectué se justifie de la manière suivante. Tous d’abord nous disposons de terminaux en 256 couleurs au laboratoire et il nous a fallu quantifier de nouveau l’image pour l’afficher (introduction de bruit de quantification). De plus les moyens d’affichage sont à matrice carrée, et il faut effectuer une nouvelle interpolation lors de l’affichage. Le contenu des images est généralement à décroissance de spectre en 1/f, il y a peu de risque de repliement de spectre.

Une seule couleur par pixel engendre une perte de luminosité, en effet les faisceaux d’électrons qui balayent l’écran auront une énergie par pixel trois fois moins grande. L’affichage d’une structure hexagonale sur écran à maillage carré impose de déformer le maillage hexagonal, il s'ensuit l’apparition de lignes verticales dans l’image. Tous ces effets cumulés ne permettent pas un bon affichage de l’image hexagonale. Il serait sans doute meilleur d’interpoler les points de couleur manquant à chaque pixel, afin d’afficher trois couleurs par pixel pour lisser l’image.

Avec tous les défauts visuels induit par l’échantillonnage hexagonal, nous avons considéré qu’une simple interpolation le long des lignes suffisait.

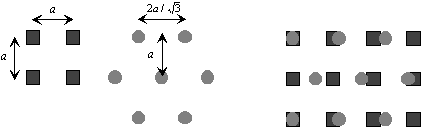
Figure 5. 50 : Méthode de conversion de maillage carré en hexagonal.

Une fois que le choix du maillage hexagonal est réalisé, il convient de choisir la méthode d’interpolation. Ce choix est une fois de plus un compromis entre temps de calcul et qualité de l’interpolation. En premier lieu nous avons choisi une méthode linéaire pour laquelle chaque point de couleur est interpolé entre les deux points de même couleur les plus poche.

Figure 5. 51 : Interpolation linéaire. Chaque point de couleur sur le maillage hexagonal est interpolé linéairement entre les deux points les plus proches sur le plan de la couleur considérée.

Nous avons également mis en place une autre méthode d’interpolation, basée sur la transformée de Fourier d’un signal discret. La transformée de Fourier discrète est périodique, de période , étant la période d’échantillonnage. Si nous modifions la périodicité du spectre de la transformée de Fourier discrète par filtrage, nous obtenons une interpolation dans le domaine spatial. Pour cette méthode, nous avons considéré que était une bonne approximation de . Il suffit donc de multiplier le nombre d’échantillon par 6 et d’effectuer un sous échantillonnage de 1 sur 7.

Nous avons réalisé la multiplication du nombre d’échantillons par 6 en deux étapes, multiplication par 2, puis multiplication par 3, à l’aide de deux filtres interpolateurs. La figure suivante montre les différentes étapes de l’interpolation par filtrage.

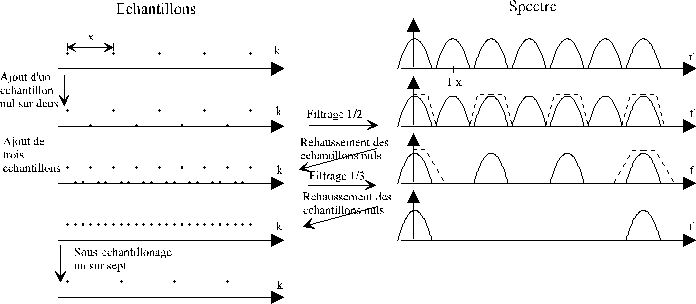
Figure 5. 52 : Méthode d’interpolation par filtrage.

La transformée de Fourier discrète d’un signal échantillonné est donnée par la relation suivante :

(5.1.1)

Il suit que est périodique de période 1/x. Si nous ajoutons un échantillon sur deux dans le signal d’origine, le spectre n’est pas modifié. Par contre si nous filtrons ensuite le signal de manière à réduire la périodicité du spectre de 1/2, les échantillons nuls sont rehaussés de manière à interpoler le signal.

Le filtre que nous avons choisi a cette étape est le suivant :

(5.1.2)

Ce filtre correspond à la convolution par le noyau suivant :

De la même manière si nous ajoutons encore deux échantillons dans les signaux obtenus par un premier filtrage, nous ne modifions pas le spectre. Nous filtrons ensuite ce signal pour rehausser les échantillons ajoutés. Le deuxième filtre que nous avons choisi est :

(5.1.3)

Ce filtre correspond à la convolution avec le noyau suivant :

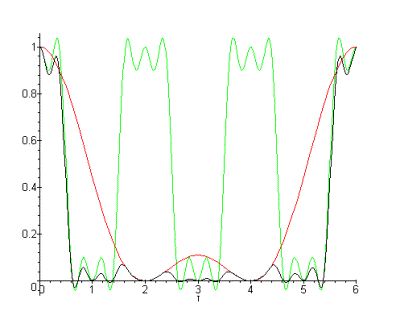
Figure 5. 53 : Les filtres d’interpolation F1,F2 et F1*F2.

Nous réalisons ensuite un sous échantillonnage de un point sur sept pour obtenir le pas d’interpolation que nous avons souhaité. Le dernier filtrage peut-être associé au sous échantillonnage en rehaussant uniquement les échantillons qui seront utiles dans le signal final. Il convient également de choisir, lors du sous échantillonnage, les échantillons dans le plan de couleur correspondant à la couleur souhaitée dans le plan hexagonal final.

Nous pensons que cette dernière méthode d’interpolation s’avère très efficace pour des processeurs de traitement de signal (DSP) qui intègrent des opérations de convolution particulièrement efficaces. Ceux-ci permettraient sans doute de réaliser une acquisition et interpolation sur maillage hexagonal en temps réel.

L’interpolation linéaire est une méthode du premier ordre qui a l’inconvénient de rendre le signal continu interpolé non dérivable, tandis que la méthode d’interpolation par filtrage est du même ordre que le noyau de convolution. Il serait préférable pour une meilleure interpolation d’utiliser des fonctions d’ordre de dérivation plus élevé. Par exemple la décomposition des signaux par fonctions splines d’ordre n serait sans doute préférable.

1.14. Implantation du modele de retine.

Nous avons implanté dans le simulateur le modèle de rétine correspondant au modèle b sur maillage hexagonal (voir chapitre 4). Les suites d’images en sortie d’un système d’acquisition vidéo ne sont pas en continues, il convient alors de discrétiser la variable temporelle. Dans nos fonctions de transfert (couche des cônes et horizontales) nous devons calculer les dérivées temporelles des signaux. Une première approximation de cette dernière est donnée par :

(5.2.1)

Reprenons l’équation du filtrage (4.1.6) en remplaçant la dérivée temporelle par son approximation (5.2.1) :

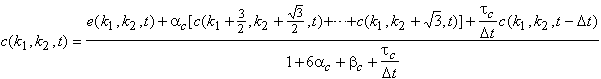(5.2.2)

Posons

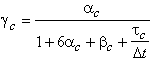et

Nous obtenons :

(5.2.3)

Où représente la somme du signal d’entrée et du signal de sortie au temps précédent. En appliquant les transformées en Z suivant les variables et , nous obtenons :

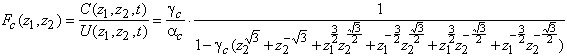(5.2.4)

La fonction est très compliquée et il est difficile de calculer directement la transformée en Z inverse. Il convient de séparer le dénominateur en produit de polynôme du premier ordre en . C’est à dire que nous allons mettre sous la forme suivante :

(5.2.5)

Pour calculer , nous imposons que les deux formes de la fonction de transfert soient égales à fréquences nulles, c’est à dire pour . Nous obtenons par ce critère :

(5.2.6)

La stabilité du filtrage est donnée par la condition qui est toujours vérifiée car . Pour normaliser le gain du filtre il faut imposer .

(a) (b)

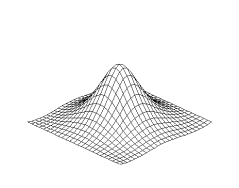
Figure 5. 54 : Comparaison des fonctions de transfert pour =0.1 (a) fonction (b) fonction approximative

En posant , , ,la fonction de transfert s’écrit finalement comme suit :

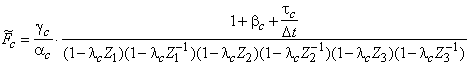(5.2.7)

Pour appliquer ce filtre il suffit de décomposer le calcul en produit de fonction du premier ordre. L’application du filtrage pour une fonction du premier ordre s’effectue de la manière suivante :

Les mêmes calculs peuvent être effectués pour le système de la couche des cellules horizontales en posant , et . Nous obtenons en définitive :

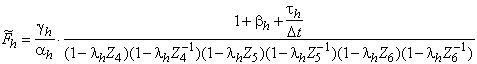(5.2.8)

Le schéma général du filtrage est alors suivant :

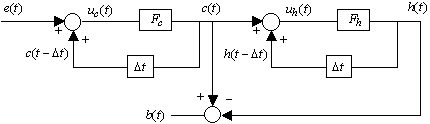
Figure 5. 55 : Filtrage spatio-temporel de la rétine.

Le filtrage spatial s’effectue en cumulant les convolutions dans les directions définies par les décalages , de manière causale et anticausale. La représentation des images en mémoire se fait par une matrice carrée. Nous avons donc adopté une convention pour représenter notre maillage hexagonal par une matrice carrée. La première valeur dans la matrice correspond à un point du maillage hexagonal et représente un point rouge. Le premier point de la ligne suivante est un point du maillage hexagonal décalé de 1/2. En fait une ligne sur deux de la matrice représente une ligne du maillage hexagonal décalée de 1/2. La notion de voisinage spatiale est alors un peu particulière pour ce type de représentation. Nous avons représenté sur la figure suivante les voisinages hexagonaux et leur représentation dans une matrice carrée pour les types de voisinages impliqués dans le filtrage rétinien.

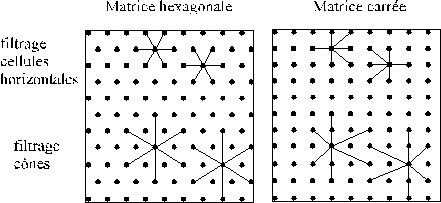
Figure 5. 56 : Polymorphie du voisinage hexagonal dans une matrice carrée. Il faut distinguer les lignes paires des lignes impaires.

Revenons sur l’approximation de la dérivée temporelle que nous avons faite[7] (5.2.1).

Comparons alors la transformée de Laplace dans l’espace continu à la transformée en Z dans l’espace discret.

Cette approximation revient à considérer la variable dans l’espace de Laplace comme étant égale à . Dans l’espace de Laplace est défini pour . Voyons alors ce qu’il advient de .

Nous avons représenté sur la figure suivante l’évolution de dans le plan complexe pour l’intervalle de considéré.

Figure 5. 57 : Evolution de z dans l’espace complexe. Avec l’approximation temporelle effectuée z évolue sur le petit cercle au lieu du cercle unité.

Cependant la correspondance entre la transformée de Fourier discrète et la transformée en Z impose , c’est à dire évoluant sur le cercle unité dans l’espace complexe.

Une autre manière de définir l’approximation de la dérivée temporelle est de considérer l’intégration discrète.

C’est à dire :

(5.2.9)

Avec cette définition parcours le cercle unité lors que .Voyons ce qu’il advient des fonctions de transfert (4.1.7) de la couche des cônes et des cellules horizontales en appliquant la relation (5.2.9). Pour simplifier l’écriture nous avons noté le filtrage spatial et pour généraliser aux deux couches, nous avons appelé l’entrée de la couche et la sortie de celle-ci.

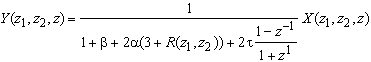
En développant cette dernière relation nous pouvons écrire :

Appliquons la transformée inverse par rapport à la variable et regroupons les termes de filtrage spatial :

Appliquons la transformée inverse par rapport à et , appelons le filtrage spatial sur le signal .

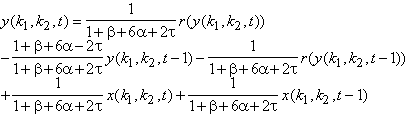
Le schéma de filtrage pour chaque couche dans le cas de cette approximation de la dérivée temporelle est alors le suivant :

Figure 5. 58 : Filtrage de chaque couche pour une approximation temporelle bi-linéaire.

A.Torralba [16] a étudié une implantation du filtre spatial rétinien par filtrage itératif. Cette méthode est particulièrement bien adaptée pour la machine CNAPS dont nous disposons au laboratoire. Cette machine de type SIMD possède 256 processeurs cadencés à 15Mhz et fonctionnant en parallèle. Elle peut effectuer 3.84 billions de multiplications/accumulations par seconde pour l’ensemble des processeurs et possède 32Mb de mémoire pour les fichiers.

L’implantation itérative du filtrage se fait de la manière suivante. Reprenons (5.2.3) en indiçant les différents points de l’image :

(5.2.10)

La sortie au point (0,0) à l’itération est fonction de l’entrée et des sorties des points voisins à l’itération . Si nous stockons une ligne par processeur, chacun sera responsable du traitement d’une ligne en parallèle avec les autres processeurs.

A.Torralba explique que l’initialisation des processeurs au temps doit être faite par le résultat du filtrage au temps . De cette manière le nombre d’itération pour établir la convergence à une erreur donnée près est fortement diminué.

Le principal défaut de la machine CNAPS est que les temps de transmission des images entre les processeurs et la machine hôte sont très grands par rapport au temps de traitement proprement dits. Ce handicap rend la machine CNAPS moins performante que la machine SUN SPARC 10 dans certains cas. Il faut que la masse de calcul devienne très importante pour que l’utilisation de la machine CNAPS soit intéressante.

1.15. Description.

Le traitement rétinien implanté dans le simulateur correspond aux fonctions de transfert (5.2.7) pour la couche des cellules réceptrices et (5.2.8) pour la couche des cellules horizontales. Le schéma de filtrage de la PLE correspondant est celui qui est représenté (figure 4.7). Une autre étude spécifique permettrait d’implanter les autres techniques de calculs expliquées dans le paragraphe précédent (approximation bilinéaire et filtrage spatial itératif), et même d’autres modèles de rétine (Chapitre 3 et 4). La figure suivante représente le schéma général du filtrage implanté dans le simulateur.

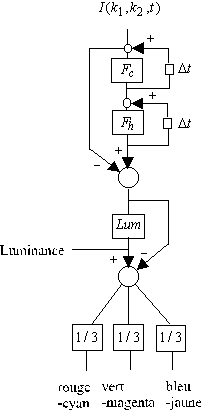
Figure 5. 59 : Schéma général du traitement rétinien dans le simulateur.

L’acquisition de séquences d’images réelles est possible à partir d’une machine de type PC équipée d’une carte d’acquisition vidéo reliée à une caméra et un moniteur couleur. Pour le moment ce système d’acquisition n’est pas en temps réel et les images sont transmises à la vitesse de transmission (Canal DMA) entre la carte et la mémoire du PC. Cependant cette carte est équipée d’un processeur DSP qui pourrait permettre l’acquisition, la conversion et peut-être même le filtrage rétinien en temps réel. C’est pour cette raison que nous avons décrit la possibilité d’une conversion de maillage par filtrage convolutif particulièrement adapté au processeur de type DSP.

La simulation a été réalisée sur machine SUN sous l’environnement graphique OPENWINDOW. Le menu principal est composé de trois sous-menus :

· File : Permet la lecture, la fermeture de séquences d’images préalablement enregistrées au format .tirf. Les images peuvent provenir du système d’acquisition de la plate forme PC au format .crt ou .flm[8]. Les images sur maillage carre ou sur maillage hexagonal peuvent être lues. Les images sur maillage hexagonal ont l’extension suivante file.hexa.tirf. Ce menu permet également de quitter l’application.

· Tools : Intègre les outils de conversion du maillage carré au maillage hexagonal, ainsi que le traitement rétinien. Nous avons également envisagé de créer une analyse FFT sur des images hexagonales en couleur, elle sera réalisée ultérieurement.

· Synthèse : Permet de créer des séquences d’images synthétiques. Création d’une séquence, ajout de deux séquences à la suite, somme de deux séquences, mise en séquence d’une image fixe.

Figure 5. 60 : Menu principal du simulateur.

Pour la conversion de maillage carré à maillage hexagonal, il y a plusieurs configurations possibles, comme le montre la figure suivante.

Figure 5. 61 : Configuration de la conversion de maillage carré au maillage hexagonal.

La case à cocher Filtrage ? signifie que l’on désire effectuer un filtrage anti-aliasing avant la conversion, avec le noyau de convolution [1 2 3 2 1] qui comme nous l’avons vu est un filtre passe-bas coupant à 1/3 de la fréquence de coupure. Le type de conversion correspond à l’approximation linéaire ou par filtrage conformément à la description que nous en avons fait plus haut (pages 50-51).

La configuration des paramètres du filtrage rétinien fait intervenir le panneau suivant.

Figure 5. 62: Configuration du filtrage spatio-temporel de la rétine.

Pour chaque couche de la rétine, il est possible d’afficher et de sauver dans un fichier les résultats du calcul. Les paramètres de chaque couche sont également configurables. Les paramètres a et b représentent la proportion de signal de la couche des cônes et cellules horizontales envoyée sur les bipolaires. Il est également possible de visualiser les canaux d’opposition de couleur et de luminance démodulés conformément aux calculs expliqués dans le chapitre 4. Le nombre d’itérations d’adaptation offre la possibilité d’adapter la rétine à la première image de la séquence.

La partie création d’images se présente sous la forme suivante.

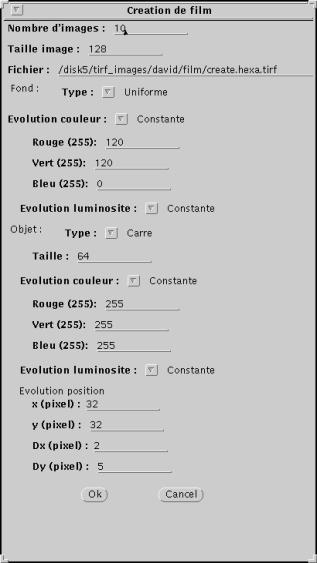
Figure 5. 63 : Configuration de la création de séquences d’images.

Nous avons créé un module de synthèse de séquences d’images pour avoir la possibilité de contrôler celles-ci au point de vue de leur composition en luminance et chrominance de manière à visualiser les propriètés décrites au chapitre 4. La synthèse est réalisée directement sur maillage hexagonal pour s’affranchir des effets de la conversion. La séquence est constituée d’un fond et d’un objet. Il est possible de contrôler la forme du fond ( uniforme, sinusoïdal ) et la forme de l’objet (carre, cercle, ...). Il est également possible de contrôler l’évolution des couleurs de l’objet ( constant, linéaire rouge, linéaire vert, quadratique rouge, ... ) à partir d’une couleur de base, l’évolution de sa luminosité (constante, linéaire, ...), et l’évolution de sa position. De la même manière il est possible de contrôler l’évolution de la couleur et de la luminosité du fond.

La figure suivante montre un exemple de création d’une séquence composée de 10 images de taille 64 contenant un carré dont la luminosité et la position évolue.

Figure 5. 64 : Exemple de création de séquence.

Le rendu d’image n’est pas excellent, à cause du conflit de table des couleurs entre les différentes applications. Pour cette raison nous avons créé le bouton Save as ppm qui permet la sauvegarde des images au format ppm, et ensuite la conversion au format désiré. Nous avons choisi deux façons d’afficher les séquences d’images dans le simulateur, la première où toutes les images sont dépliées comme pour la figure précédente, et le seconde ou l’on visualise le film des images superposées les unes à la suite des autres. Le bouton Film permet de jouer la séquence d’images, et dans l’autre mode d’affichage un bouton Planche permet de revenir en mode planche et un bouton Replay permet de rejouer le film.

La programmation du simulateur a nécessité plus de 5000 lignes de code C réparties en 4 modules. La partie gestion de l’interface graphique comprend environ 700 lignes. La partie manipulation des fichiers et affichage graphique 2700 lignes. La partie traitement rétinien proprement dit 1500 lignes. Enfin la partie synthèse d’images 700 lignes.

Les temps d’exécution permettent une simulation relativement rapide, bien que très éloignée du temps réel. Le traitement rétinien appliqué à une séquence de 20 images de tailles 128x110 est éffectué en 1mn 20s si l’on choisi d’afficher toutes les fenètres de traitement intermédiaire. Ce temps est ramené à 30s si l’on choisit d’afficher seulement la fenètre de reconstruction. La synthèse d’une image est effectuée en 2 ou 3 secondes. La lecture et l’affichage d’une image 512x512 au format tirf sont effectués en 2s. La conversion d’une image du maillage carré au maillage hexagonal dure 3s par la méthode d’interpolation linéaire, et 10s par la méthode de filtrage.

L’extension du simulateur pourrait prendre deux directions. La première consisterait à terminer et à tester les différentes parties qui n’ont pas encore été mise en place ( autres implémentations du filtrage rétinien, autres modèles, FFT, autres créations de séquences ). La deuxième serait un outil de mesure directe dans l’image obtenu de la valeur du pixel, pour comparer les résultats avec les mesures effectuées par les neuro-physiologistes.

conclusion

Nous pouvons distinguer deux objectifs différents en traitement d’images : la transmission ou l’interprétation d’images. Le premier cherche à réduire la quantité d’information à transmettre, tout en assurant une reconstruction de l’image d’origine. Le deuxième cherche également à réduire l’information mais pour former une classification des informations pertinentes. Nos modèles permettent plutôt l’interprétation d’images, bien que les propriétés du système visuel qu’ils imitent trouvent des applications dans la transmission.

La validation de notre modèle est essentiellement réalisée par la confrontation de ses résultats avec la psychophysiologie. En particulier le phénomène de désaturation que nous avons pu observer avec le simulateur, en recomposant les canaux d’opposition de couleur, permet de valider le modèle pour des cas simples. De même les simulations que nous avons réalisé montre que ce modèle reste très efficace pour le traitement du mouvement. Ces deux propriètés sont en fait liées, elles représente le traitement temporel des signaux. Nous pouvons considérer que le modèle est valide pour le traitement temporel bien que la constance des couleurs ne soit pas vraiment expliqué. Cependant de nouveaux éléments permettent de penser que la constance des couleurs peut s’expliquer par une modulation des résistances de couplages entre les couches de la rétine.

Il reste tout de même un bon nombre de particularité psychophysiologique qui ne sont pas expliquées par notre modèle de rétine chromatique. Par exemple nous ne pouvons pas modéliser et expliquer le fait que les récepteurs bleu soit absents de la fovea centrale alors que notre acuité à dicerner la couleur bleu au centre d’une image n’est pas nul. De même nous savons par la biologie que le traitement rétinien n’est pas uniforme et varie en fonction de l’éloignement de l’axe optique. La variation touche essentiellement l’échantillonnage et les types de connexions entre les cellules.

Pour tenir compte de ces modifications spatiales, il faut réaliser un modèle plus global de la rétine. Pour cela nous envisageons de découper l’étude de la rétine en plusieurs parties et d’analyser les interactions entre ces parties. Il faut ensuite trouver un modèle plausible pour chaque partie de la rétine, et un modèle d’interaction entre les différentes parties. L’avantage de cette décomposition est de pouvoir tenir compte de l’échantillonnage variable de la rétine et des propriètés variables des modèles de chacune des parties. Les différentes possibilités de transposition du modèle à deux cônes par cellules horizontales sur maillage hexagonal developpé au chapitre quatre, permettent de tenir compte des spécificités de ces parties de rétine. En particulier la répartition variable des types de récepteurs, et la spécialisation des cellules horizontales à la couleur peuvent être pris en compte.

Ce modèle de la vision des couleurs, bien que simpliste relève déja des particularités du système visuel qui pourrait être exploitées en compression ou en synthèse d’images. Notament la réponse temporelle particulière aux stimulis colorés peut permettre une simplification de l’animation des scènes en synthése d’image, ou une compression des séquences d’images.

---

[1] La variété du type de récepteur d’un individu à l’autre, ne remet pas en question les lois fondamentales de la colorimètrie. Il est alors possible que le traitement de la couleur dans le système de vision s’effectue de manière à s’affranchir de ces disparités.

[2]C’est à dire qu’on ne peut reproduire une couleur à partir des deux autres.

[3]Le cyan est une couleur entre le vert et le bleu. Le magenta entre le bleu et rouge.

[4] Cela revient à supprimer les connexions entre les cellules de la couche des cônes. C’est à dire que nous revenons au modèle avec une rétroaction des cellules horizontales sur l’entrée.

[5] Pour simplifier la représentation et le discours nous avons volontairement omis de mentionner la variable temporelle. Cependant il faut en tenir compte.

[6] Nous avons omis la variable temporelle t pour simplifier les écritures. Cependant les signaux dépendent du temps

[7]Pour simplifier l’écriture nous avons posé .

[8]Les formats .crt, .flm, .tirf ont été créés par W.Beaudot. Seule l’extension .hexa.tirf à été réalisée pour permettre la compatibilité avec les images au format hexagonal.

---

[C1]